题目内容
(本小题14分)已知函数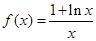
(Ⅰ)若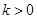 且函数
且函数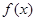 在区间
在区间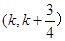 上存在极值,求实数
上存在极值,求实数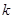 的取值范围;
的取值范围;
(Ⅱ)如果当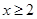 时,不等式
时,不等式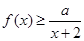 恒成立,求实数
恒成立,求实数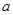 的取值范围;
的取值范围;
(Ⅲ)求证: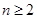 ,
,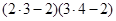 ……
……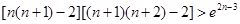 .
.
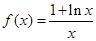
(Ⅰ)若
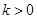 且函数
且函数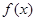 在区间
在区间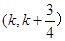 上存在极值,求实数
上存在极值,求实数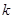 的取值范围;
的取值范围;(Ⅱ)如果当
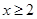 时,不等式
时,不等式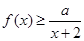 恒成立,求实数
恒成立,求实数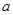 的取值范围;
的取值范围;(Ⅲ)求证:
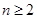 ,
,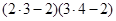 ……
……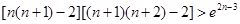 .
.(Ⅰ)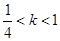 ;(Ⅱ)
;(Ⅱ)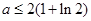 ;(Ⅲ)见解析。
;(Ⅲ)见解析。
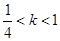 ;(Ⅱ)
;(Ⅱ)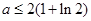 ;(Ⅲ)见解析。
;(Ⅲ)见解析。本试题主要是考查了导数在研究函数中的运用。求解函数的极值,和不等式的恒成立问题,以及证明不等式。
解:(Ⅰ)因为
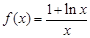 , x
, x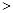 0,则
0,则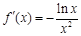 ,
,
求解导数,判定函数单调性,得到极值。
因为函数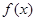 在区间
在区间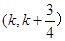 (其中
(其中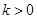 )上存在极值,
)上存在极值,
得到参数k的范围。
(Ⅱ)不等式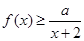 ,又
,又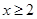 ,则
,则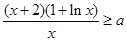 ,构造新函数
,构造新函数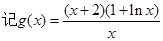 ,则
,则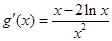
令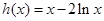 ,则
,则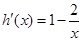 ,
,
分析单调性得到证明。
(Ⅲ)由(2)知:当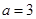 时,
时,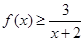 恒成立,即
恒成立,即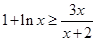 ,
,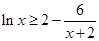 ,
,
令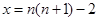 ,则
,则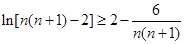 ;可以证明。
;可以证明。
解:(Ⅰ)因为
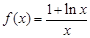 , x
, x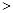 0,则
0,则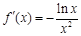 ,
,
当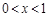 时,
时,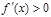 ;当
;当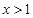 时,
时,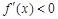 .
.
所以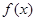 在(0,1)上单调递增;在
在(0,1)上单调递增;在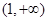 上单调递减,
上单调递减,
所以函数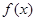 在
在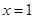 处取得极大值;……….2分
处取得极大值;……….2分
因为函数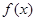 在区间
在区间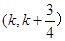 (其中
(其中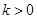 )上存在极值,
)上存在极值,
所以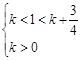 解得
解得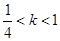 ;……….4分
;……….4分
(Ⅱ)不等式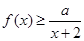 ,又
,又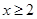 ,则
,则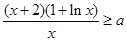 ,
,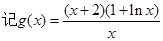 ,则
,则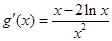 ;……….6分
;……….6分
令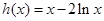 ,则
,则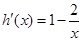 ,
,
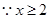 ,
,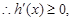
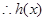 在
在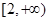 上单调递增,
上单调递增,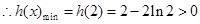 ,
,
从而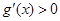 , 故
, 故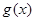 在
在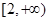 上也单调递增, 所以
上也单调递增, 所以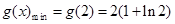 ,
,
所以.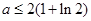 ;……….8分
;……….8分
(Ⅲ)由(2)知:当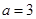 时,
时,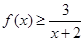 恒成立,即
恒成立,即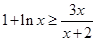 ,
,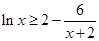 ,
,
令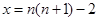 ,则
,则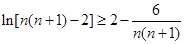 ;……….10分
;……….10分
所以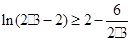 ,
,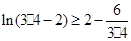 ,……
,……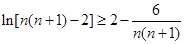
,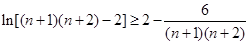
n个不等式相加得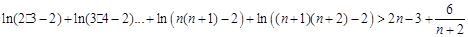
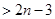
即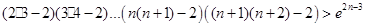 ……….14分
……….14分
解:(Ⅰ)因为

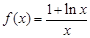 , x
, x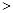 0,则
0,则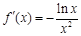 ,
,求解导数,判定函数单调性,得到极值。
因为函数
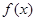 在区间
在区间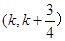 (其中
(其中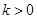 )上存在极值,
)上存在极值,得到参数k的范围。
(Ⅱ)不等式
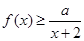 ,又
,又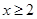 ,则
,则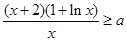 ,构造新函数
,构造新函数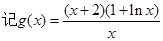 ,则
,则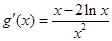
令
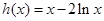 ,则
,则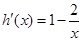 ,
,分析单调性得到证明。
(Ⅲ)由(2)知:当
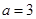 时,
时,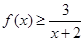 恒成立,即
恒成立,即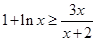 ,
,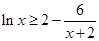 ,
,令
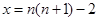 ,则
,则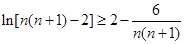 ;可以证明。
;可以证明。解:(Ⅰ)因为

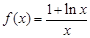 , x
, x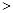 0,则
0,则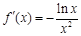 ,
,当
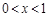 时,
时,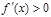 ;当
;当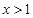 时,
时,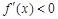 .
.所以
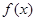 在(0,1)上单调递增;在
在(0,1)上单调递增;在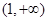 上单调递减,
上单调递减,所以函数
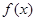 在
在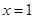 处取得极大值;……….2分
处取得极大值;……….2分因为函数
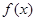 在区间
在区间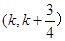 (其中
(其中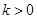 )上存在极值,
)上存在极值,所以
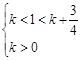 解得
解得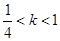 ;……….4分
;……….4分(Ⅱ)不等式
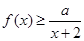 ,又
,又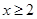 ,则
,则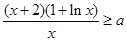 ,
,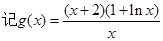 ,则
,则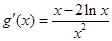 ;……….6分
;……….6分令
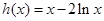 ,则
,则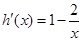 ,
,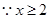 ,
,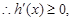
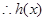 在
在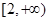 上单调递增,
上单调递增,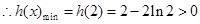 ,
,从而
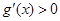 , 故
, 故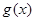 在
在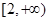 上也单调递增, 所以
上也单调递增, 所以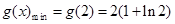 ,
,所以.
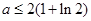 ;……….8分
;……….8分(Ⅲ)由(2)知:当
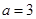 时,
时,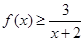 恒成立,即
恒成立,即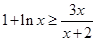 ,
,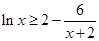 ,
,令
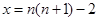 ,则
,则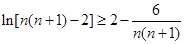 ;……….10分
;……….10分所以
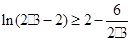 ,
,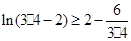 ,……
,……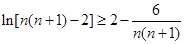
,
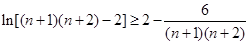
n个不等式相加得
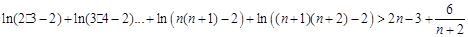
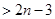
即
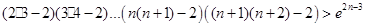 ……….14分
……….14分
练习册系列答案
相关题目
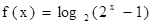 ,
,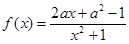 ,其中
,其中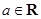 .
.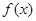 的单调区间;
的单调区间;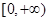 上存在最大值和最小值,求
上存在最大值和最小值,求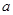 的取值范围.
的取值范围. ]
]

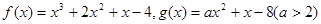 .
.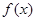 的极值;
的极值;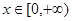 ,都有
,都有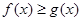 ,求实数a的取值范围.
,求实数a的取值范围.
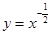
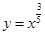
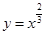
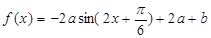 ,
,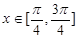 ,是否存在常数
,是否存在常数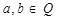 时,使得
时,使得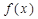 的值域为[
的值域为[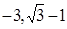 ]?若存在,求出
]?若存在,求出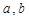 的值,若不存在,说明理由。
的值,若不存在,说明理由。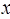 的方程
的方程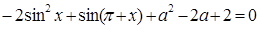 在
在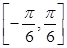 内有实数根,求实数
内有实数根,求实数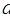 的范围。
的范围。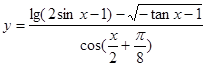 的定义域_____________
的定义域_____________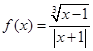 的定义域。
的定义域。