题目内容
已知函数 ,对于n∈N+,定义f1(x)=f(x),fn+1(x)=f[fn(x)],偶函数g(x)的定义域为{x|x≠0},
,对于n∈N+,定义f1(x)=f(x),fn+1(x)=f[fn(x)],偶函数g(x)的定义域为{x|x≠0},当x>0时,g(x)=|f2009(x)|.
(1)求g(x);
(2)若存在实数a,b(a<b)使得该函数在[a,b]上的最大值为ma,最小值为mb,求非零实数m的取值范围.
【答案】分析:(1)根据已知条件推导出迭代函数以3为周期,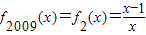 .由此能求出求g(x).
.由此能求出求g(x).
(2)因为a<b,ma>mb>0,所以m<0,a<b<0;因为mb≠0,所以-1∉[a,b].所以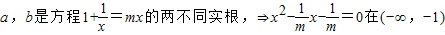 有两个不同实根,由此能求出非零实数m的取值范围.
有两个不同实根,由此能求出非零实数m的取值范围.
解答:解:(1)因为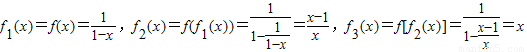
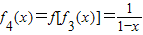 ,
,
∴迭代函数以3为周期,
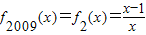 .…(5分)
.…(5分)
设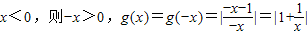 ,
,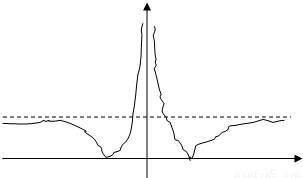
所以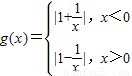 …(9分)
…(9分)
如图:
(2)∵a<b,ma>mb>0
∴m<0,a<b<0;…(12分)
∵mb≠0,
∴-1∉[a,b](否则m=0,mb=ma=0,矛盾),
当 ,
,
所以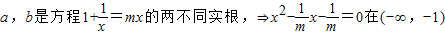 有两个不同实根,
有两个不同实根,
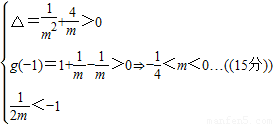

综上所述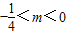 .(19分).
.(19分).
点评:本题考查函数的周期性和函数最值的应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.易错点是综合性强,难度大,基础不牢,找不准解题思路.
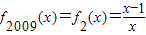 .由此能求出求g(x).
.由此能求出求g(x).(2)因为a<b,ma>mb>0,所以m<0,a<b<0;因为mb≠0,所以-1∉[a,b].所以
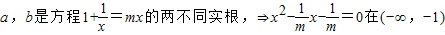 有两个不同实根,由此能求出非零实数m的取值范围.
有两个不同实根,由此能求出非零实数m的取值范围.解答:解:(1)因为
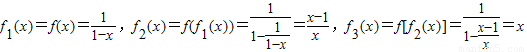
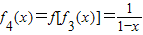 ,
,∴迭代函数以3为周期,
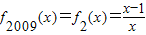 .…(5分)
.…(5分)设
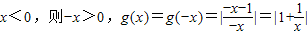 ,
,
所以
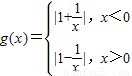 …(9分)
…(9分)如图:
(2)∵a<b,ma>mb>0
∴m<0,a<b<0;…(12分)
∵mb≠0,
∴-1∉[a,b](否则m=0,mb=ma=0,矛盾),
当
 ,
,所以
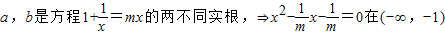 有两个不同实根,
有两个不同实根,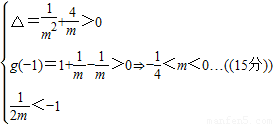

综上所述
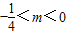 .(19分).
.(19分).点评:本题考查函数的周期性和函数最值的应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.易错点是综合性强,难度大,基础不牢,找不准解题思路.

练习册系列答案
相关题目

 ,对于n∈N*,定义fn+1(x)=f1[fn(x)],则f2011(x)=________.
,对于n∈N*,定义fn+1(x)=f1[fn(x)],则f2011(x)=________. ,对于n∈N*,定义fn+1(x)=f1[fn(x)],则f2011(x)= .
,对于n∈N*,定义fn+1(x)=f1[fn(x)],则f2011(x)= .