题目内容
 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,PC⊥面ABC,直线AM与直线PC所成的角为60°,求二面角M-AC-B的平面角的余弦值.
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,PC⊥面ABC,直线AM与直线PC所成的角为60°,求二面角M-AC-B的平面角的余弦值.分析:通过建立空间直角坐标系,利用异面直线的方向向量即可得到异面直线所成的角,求出点P的坐标,再利用两个平面的法向量即可得出二面角.
解答: 解:在平面ABC内,过C作CD⊥CB,建立空间直角坐标系C-xyz(如图)
解:在平面ABC内,过C作CD⊥CB,建立空间直角坐标系C-xyz(如图)
由题意有A(
,-
,0),设P(0,0,z0),(z0>0),
则M(0,1,z0),
=(-
,
,z0),
=(0,0,z0),
由直线AM与直线PC所成的角为60°,得
•
=|
|•|
|•cos60°,
即
=
•z0,解得z0=1,
∴
=(0,1,1),
=(
,-
,0),
设平面MAC的一个法向量为
=(x1,y1,z1),
则
,即
,取x1=1,得
=(1,
,-
).
平面ABC的法向量为
,∴cos<
,
>=
=
=-
,
又∵二面角M-AC-B为锐角,∴二面角M-AC-B的平面角余弦值为
.
 解:在平面ABC内,过C作CD⊥CB,建立空间直角坐标系C-xyz(如图)
解:在平面ABC内,过C作CD⊥CB,建立空间直角坐标系C-xyz(如图)由题意有A(
| ||
| 2 |
| 1 |
| 2 |
则M(0,1,z0),
| AM |
| ||
| 2 |
| 3 |
| 2 |
| CP |
由直线AM与直线PC所成的角为60°,得
| AM |
| CP |
| AM |
| CP |
即
| z | 2 0 |
| 1 |
| 2 |
|
∴
| CM |
| CA |
| ||
| 2 |
| 1 |
| 2 |
设平面MAC的一个法向量为
| n |
则
|
|
| n |
| 3 |
| 3 |
平面ABC的法向量为
| CP |
| CP |
| n |
| ||||
|
-
| ||
|
| ||
| 7 |
又∵二面角M-AC-B为锐角,∴二面角M-AC-B的平面角余弦值为
| ||
| 7 |
点评:熟练掌握通过建立空间直角坐标系并利用异面直线的方向向量得到异面直线所成的角、利用两个平面的法向量求二面角的方法是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°. 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
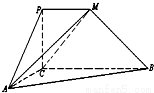 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.