题目内容
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.(1)求证:平面PAC⊥平面ABC;
(2)求二面角M-AC-B的平面角的余弦值.

【答案】分析:(1)通过证明PC⊥平面ABC,证明平面PAC⊥平面ABC;
(2)解法一:(几何法)取BC的中点N,则CN=1,连接AN,MN,说明∠MHN为二面角M-AC-B的平面角,解三角形求二面角M-AC-B的大小;
解法二:(向量法)在平面ABC内,过C作CD⊥CB,建立空间直角坐标系C-xyz,求出平面MAC的一个法向量为 ,平面ABC的法向量取为
,平面ABC的法向量取为 ,利用
,利用 ,解答即可.
,解答即可.
解答:证明:(1)∵PC⊥AB,PC⊥BC,AB∩BC=B
∴PC⊥平面ABC,…(2分)
又∵PC?平面PAC
∴平面PAC⊥平面ABC…(5分)
(2)解法一:(几何法)
取BC的中点N,则CN=1,连接AN,MN,
∵PM∥CN,PM=CN
∴MN∥PC,MN=PC,
从而MN⊥平面ABC
作NH⊥AC,交AC的延长线于H,连接MH,则由三垂线定理知,AC⊥NH,
从而∠MHN为二面角M-AC-B的平面角
直线AM与直线PC所成的角为60
∴∠AMN=60°
在△ACN中,由余弦定理得AN= =
= ;
;
在△AMN中,MN=AN•cot∠AMN= ×
× =1;
=1;
在△CNH中,NH=CN•sin∠NCH=1× =
= ;
;
在△MNH中,MN=tan∠MHN= =
= =
= ;
;
则cos∠MHN= =
=
解法二:(向量法)
在平面ABC内,过C作CD⊥CB,建立空间直角坐标系C-xyz(如图)…(6分)
由题意有 ,设P(0,0,z)(z>0),
,设P(0,0,z)(z>0),
则
由直线AM与直线PC所成的解为60,得 ,即
,即 ,
,
解得z=1…(8分)
∴ ,
,
设平面MAC的一个法向量为 ,
,
则 ,
,
取x1=1,得 …(9分)
…(9分)
平面ABC的法向量取为 …(10分)
…(10分)
设 与
与 所成的角为θ,则
所成的角为θ,则 …(11分)
…(11分)
显然,二面角M-AC-B的平面角为锐角,
故二面角M-AC-B的平面角的余弦值为 …(12分)
…(12分)
点评:本题主要考查异面直线所成的角、平面与平面垂直、二面角等有关知识,考查思维能力和空间想象能力、应用向量知识解决数学问题的能力、化归转化能力和推理运算能力.
(2)解法一:(几何法)取BC的中点N,则CN=1,连接AN,MN,说明∠MHN为二面角M-AC-B的平面角,解三角形求二面角M-AC-B的大小;
解法二:(向量法)在平面ABC内,过C作CD⊥CB,建立空间直角坐标系C-xyz,求出平面MAC的一个法向量为
 ,平面ABC的法向量取为
,平面ABC的法向量取为 ,利用
,利用 ,解答即可.
,解答即可.解答:证明:(1)∵PC⊥AB,PC⊥BC,AB∩BC=B

∴PC⊥平面ABC,…(2分)
又∵PC?平面PAC
∴平面PAC⊥平面ABC…(5分)
(2)解法一:(几何法)
取BC的中点N,则CN=1,连接AN,MN,
∵PM∥CN,PM=CN
∴MN∥PC,MN=PC,
从而MN⊥平面ABC
作NH⊥AC,交AC的延长线于H,连接MH,则由三垂线定理知,AC⊥NH,
从而∠MHN为二面角M-AC-B的平面角
直线AM与直线PC所成的角为60
∴∠AMN=60°
在△ACN中,由余弦定理得AN=
 =
= ;
;在△AMN中,MN=AN•cot∠AMN=
 ×
× =1;
=1;在△CNH中,NH=CN•sin∠NCH=1×
 =
= ;
;在△MNH中,MN=tan∠MHN=
 =
= =
= ;
;则cos∠MHN=
 =
=
解法二:(向量法)

在平面ABC内,过C作CD⊥CB,建立空间直角坐标系C-xyz(如图)…(6分)
由题意有
 ,设P(0,0,z)(z>0),
,设P(0,0,z)(z>0),则

由直线AM与直线PC所成的解为60,得
 ,即
,即 ,
,解得z=1…(8分)
∴
 ,
,设平面MAC的一个法向量为
 ,
,则
 ,
,取x1=1,得
 …(9分)
…(9分)平面ABC的法向量取为
 …(10分)
…(10分)设
 与
与 所成的角为θ,则
所成的角为θ,则 …(11分)
…(11分)显然,二面角M-AC-B的平面角为锐角,
故二面角M-AC-B的平面角的余弦值为
 …(12分)
…(12分)点评:本题主要考查异面直线所成的角、平面与平面垂直、二面角等有关知识,考查思维能力和空间想象能力、应用向量知识解决数学问题的能力、化归转化能力和推理运算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°. 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,PC⊥面ABC,直线AM与直线PC所成的角为60°,求二面角M-AC-B的平面角的余弦值.
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,PC⊥面ABC,直线AM与直线PC所成的角为60°,求二面角M-AC-B的平面角的余弦值. 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.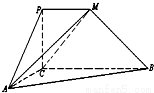 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.