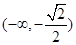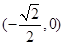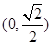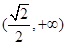题目内容
已知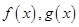 都是定义在
都是定义在 上的函数,
上的函数,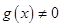 ,
,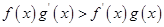 ,
,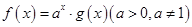 ,
,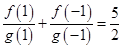 ,在有穷数列
,在有穷数列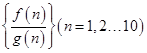 中,任意取正整数
中,任意取正整数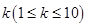 ,则前
,则前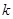 项和大于
项和大于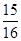 的概率是 ( )
的概率是 ( )
A.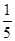 | B.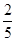 | C.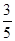 | D.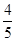 |
C
解析试题分析:由已知得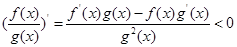 ,所以
,所以 单调递减,
单调递减,
又因为 ,所以
,所以 ,所以
,所以 ,所以
,所以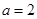 (舍)或
(舍)或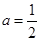 ,
,
所以 (舍)或
(舍)或 ,当
,当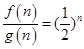 时,数列
时,数列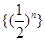 中,
中, ,所以
,所以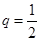 ,
,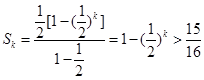 ,所以
,所以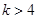 ,又因为
,又因为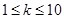 即
即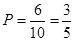 .
.
考点:1.用导数判断函数的单调性;2.等比数列的求和公式;3.几何概型.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
已知二次函数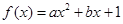 的导数为
的导数为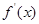 ,
,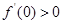 ,
, 与
与 轴恰有一个交点,则
轴恰有一个交点,则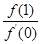 的最小值为( )
的最小值为( )
| A.3 | B.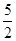 | C.2 | D.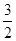 |
曲线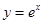 在点
在点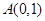 处的切线为( )
处的切线为( )
A.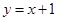 | B.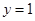 | C.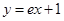 | D.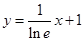 |
函数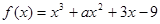 ,已知
,已知 在
在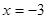 时取得极值,则
时取得极值,则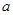 =( )
=( )
| A.2 | B.3 | C.4 | D.5 |
已知函数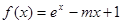 的图像为曲线C,若曲线C存在与直线
的图像为曲线C,若曲线C存在与直线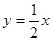 垂直的切线,则实数m的取值范围是( )
垂直的切线,则实数m的取值范围是( )
A. | B.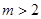 | C.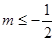 | D. |
边界在直线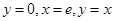 及曲线
及曲线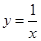 上的封闭的图形的面积为( )
上的封闭的图形的面积为( )
| A.1 | B. | C.2 | D.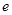 |
已知函数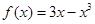 ,当
,当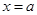 时取得极小值
时取得极小值 ,则
,则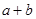 等于( )
等于( )
A. | B. | C.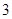 | D.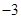 |
设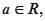 函数
函数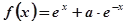 的导函数是
的导函数是 且
且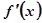 是奇函数,若曲线
是奇函数,若曲线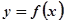 的一条切线的斜率是
的一条切线的斜率是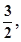 则切点的横坐标为( )
则切点的横坐标为( )
A. | B.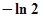 | C.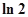 | D. |
 的导函数为
的导函数为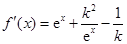 (其中
(其中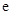 为自然对数的底数,
为自然对数的底数, 为实数),且
为实数),且 在
在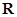 上不是单调函数,则实数
上不是单调函数,则实数