��Ŀ����
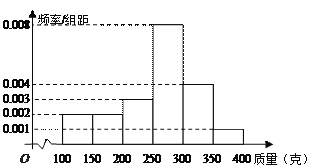
����Ŀ������Լ��ˮ���Թ����������л������������ͳ��ij��ͳ�ƾֵ����˸����ڶ��ͥ����ˮ�����������������ˮ����Ƶ�ʷֲ�ֱ��ͼ������ͼ��ʾ��������ˮ����������Ƶ����Ϊ���ʣ�������ÿ�����ˮ���������

��l������δ������3�����������2���µ�����ˮ����������12������1���µ�����ˮ������4�ֵĸ��ʣ�
��2����![]() ��ʾ��δ��3����������ˮ��������12�ֵ�����������軱���
��ʾ��δ��3����������ˮ��������12�ֵ�����������軱���![]() �ķֲ��м���ѧ����
�ķֲ��м���ѧ����![]() ��
��
���𰸡���1��0.027����2��������
����������������1������������¼��˷����ʹ�ʽ�ͻ����¼��ӷ���ʽ�������δ������3�����������2���µ�����ˮ����������12������1���µ�����ˮ������4�ֵĸ��ʣ�
��2���������X�Ŀ���ȡֵΪ0��1��2��3����X����3��0.3�����ɴ�������������X�ķֲ�����ѧ����E��X����
�������1����![]() ��ʾ�¼�������ˮ��������12�֡���
��ʾ�¼�������ˮ��������12�֡���![]() ��ʾ�¼�������ˮ������4�֡���
��ʾ�¼�������ˮ������4�֡���![]() ��ʾ�¼�����δ������3�����������2���µ�����ˮ����������12������1���µ�����ˮ������4�֡�.
��ʾ�¼�����δ������3�����������2���µ�����ˮ����������12������1���µ�����ˮ������4�֡�.
��ˣ�![]() ��
��![]() .
.
��Ϊÿ�����ˮ���������
����![]() .
.
��2��![]() ����ȡ��ֵΪ0,1,2,3��
����ȡ��ֵΪ0,1,2,3��
��Ӧ�ĸ��ʷֱ�Ϊ

![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
��![]() �ķֲ���Ϊ
�ķֲ���Ϊ
��![]() ����ѧ����Ϊ
����ѧ����Ϊ![]()
![]() .
.

 ������������ϵ�д�
������������ϵ�д�����Ŀ��Ϊ���о�ij��ϸ����ʱ��x�仯����ֳ�ĸ������ռ��������£�
![]()
��1�������������ͱ�������ֳ������Ԥ��������������Щ���ݵ�ɢ��ͼ������ɢ��ͼ�жϣ�![]() ��y=
��y=![]() ��һ����Ϊ��ֳ�ĸ���y����ʱ��x�仯�Ļع鷽������Ϊ��ѣ��������жϼ��ɣ�����˵�����ɣ�
��һ����Ϊ��ֳ�ĸ���y����ʱ��x�仯�Ļع鷽������Ϊ��ѣ��������жϼ��ɣ�����˵�����ɣ�
|
|
|
|
|
|
3.5 | 62��83 | 3.53 | 17.5 | 596.505 | 12.04 |
����![]() ��
��![]()
��2�����ݣ�1�����ж���ѽ�������е����ݣ�����y����x �Ļع鷽�̡�
�ο���ʽ�� 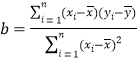
![]()