题目内容
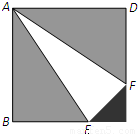
 某人为装修房屋,需定制一批瓷砖,要求用三种不同材质制成面积为1m2的正方形大瓷砖ABCD(如图).其中,△EFC为等腰直角三角形,△ABE≌△ADF.三种材质△EFC、△ABE(△ADF)、△AEF每平方米的价格分别为260元、100元、60元.若正方形大瓷砖每平方米的价格为y(元),等腰直角△EFC的直角边长为x(m).
某人为装修房屋,需定制一批瓷砖,要求用三种不同材质制成面积为1m2的正方形大瓷砖ABCD(如图).其中,△EFC为等腰直角三角形,△ABE≌△ADF.三种材质△EFC、△ABE(△ADF)、△AEF每平方米的价格分别为260元、100元、60元.若正方形大瓷砖每平方米的价格为y(元),等腰直角△EFC的直角边长为x(m).(1)求y关于x的函数,并指出函数的定义域;
(2)当x为何值时,正方形大瓷砖每平方米的价格最低?
分析:(1)利用直角三角形的面积公式及其价格即可得出解析式;
(2)通过配方利用二次函数的单调性即可得出.
(2)通过配方利用二次函数的单调性即可得出.
解答:解:(1)y=
x2×260+
×1×(1-x)×100×2+[1-
x2-(1-x)]×60
=130 x2+100-100x-30 x2+60x
=100 x2-40x+100,其中,x∈(0,1).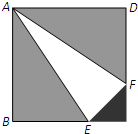
(2)y=100(x2-
x)+100=100(x-
)2+96,
∴当x=
时,ymin=96.
答:当x=
时,正方形大瓷砖每平方米的价格最低,为96元.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=130 x2+100-100x-30 x2+60x
=100 x2-40x+100,其中,x∈(0,1).

(2)y=100(x2-
| 2 |
| 5 |
| 1 |
| 5 |
∴当x=
| 1 |
| 5 |
答:当x=
| 1 |
| 5 |
点评:正确理解题意和熟练掌握三角形的面积计算公式、二次函数的单调性等是解题的关键.

练习册系列答案
相关题目

 某人为装修房屋,需定制一批瓷砖,要求用三种不同材质制成面积为1m2的正方形大瓷砖ABCD(如图).其中,△EFC为等腰直角三角形,△ABE≌△ADF.三种材质△EFC、△ABE(△ADF)、△AEF每平方米的价格分别为260元、100元、60元.若正方形大瓷砖每平方米的价格为y(元),等腰直角△EFC的直角边长为x(m).
某人为装修房屋,需定制一批瓷砖,要求用三种不同材质制成面积为1m2的正方形大瓷砖ABCD(如图).其中,△EFC为等腰直角三角形,△ABE≌△ADF.三种材质△EFC、△ABE(△ADF)、△AEF每平方米的价格分别为260元、100元、60元.若正方形大瓷砖每平方米的价格为y(元),等腰直角△EFC的直角边长为x(m).