题目内容
如图,已知点P是圆上C:x2+(y-2 )2=1的一个动点,点Q是直线l:x-y=0上的一个动点,O为坐标原点,则向量
)2=1的一个动点,点Q是直线l:x-y=0上的一个动点,O为坐标原点,则向量
 上的投影的最大值是( )
上的投影的最大值是( )
A.3
B.

C.

D.1
【答案】分析:设 夹角为θ,则向量
夹角为θ,则向量 上的投影等于
上的投影等于 cosθ=
cosθ= .分析出θ应为锐角,设P(x,y),不妨取Q(1,1),转化为求x+y的最小值问题,可以用圆的参数方程或线性规划的方法求解.
.分析出θ应为锐角,设P(x,y),不妨取Q(1,1),转化为求x+y的最小值问题,可以用圆的参数方程或线性规划的方法求解.
解答:解:设 夹角为θ,则向量
夹角为θ,则向量 上的投影等于
上的投影等于 cosθ,若取得最大值则首先θ为锐角.
cosθ,若取得最大值则首先θ为锐角.
设P(x,y),不妨取Q(1,1),则根据向量数量积的运算得出 cosθ=
cosθ= =
= ①
①
由于P是圆 上的一个动点,设
上的一个动点,设 ②
②
将②代入①得出 cosθ=
cosθ= (cosα+sinα+
(cosα+sinα+ ),而cosα+sinα的最大值为
),而cosα+sinα的最大值为 ,
,
所以 cosθ≥
cosθ≥ =3
=3
故选A.
点评:本题考查向量投影的计算,最值问题求解,考查转化、计算能力.
 夹角为θ,则向量
夹角为θ,则向量 上的投影等于
上的投影等于 cosθ=
cosθ= .分析出θ应为锐角,设P(x,y),不妨取Q(1,1),转化为求x+y的最小值问题,可以用圆的参数方程或线性规划的方法求解.
.分析出θ应为锐角,设P(x,y),不妨取Q(1,1),转化为求x+y的最小值问题,可以用圆的参数方程或线性规划的方法求解.解答:解:设
 夹角为θ,则向量
夹角为θ,则向量 上的投影等于
上的投影等于 cosθ,若取得最大值则首先θ为锐角.
cosθ,若取得最大值则首先θ为锐角.设P(x,y),不妨取Q(1,1),则根据向量数量积的运算得出
 cosθ=
cosθ= =
= ①
①由于P是圆
 上的一个动点,设
上的一个动点,设 ②
②将②代入①得出
 cosθ=
cosθ= (cosα+sinα+
(cosα+sinα+ ),而cosα+sinα的最大值为
),而cosα+sinα的最大值为 ,
,所以
 cosθ≥
cosθ≥ =3
=3故选A.
点评:本题考查向量投影的计算,最值问题求解,考查转化、计算能力.

练习册系列答案
相关题目
 (2011•武昌区模拟)如图,已知点P是圆上C:x2+(y-2
(2011•武昌区模拟)如图,已知点P是圆上C:x2+(y-2 (2011•武昌区模拟)如图,已知点P是圆
(2011•武昌区模拟)如图,已知点P是圆 如图,已知点P是圆
如图,已知点P是圆 上的一个动点,点Q是直线l:x-y=0上的一个动点,O为坐标原点,则向量
上的一个动点,点Q是直线l:x-y=0上的一个动点,O为坐标原点,则向量 上的投影的最大值是
上的投影的最大值是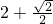

 上的一个动点,点Q是直线l:x-y=0上的一个动点,O为坐标原点,则向量
上的一个动点,点Q是直线l:x-y=0上的一个动点,O为坐标原点,则向量 上的投影的最大值是( )
上的投影的最大值是( )

