题目内容
将函数f(x)=sin2x-
cos2x的图象向左平移m个单位(m>0),(
,0)是所得函数的图象的一个对称中心,则m的最小值为( )
| 3 |
| π |
| 2 |
分析:f(x)解析式提取2变形后,利用两角和与差的正弦函数公式化为一个角的正弦函数,利用平移规律得出g(x)解析式,根据(
,0)为g(x)图象的一个对称中心,根据m大于0即可确定出m的最小值.
| π |
| 2 |
解答:解:f(x)=sin2x-
cos2x=2sin(2x-
),
向左平移m个单位得到g(x)=2sin[2(x+m)-
]=2sin(2x+2m-
),
∴g(
)=2sin(2×
+2m-
)=2sin(2m+
)=0,
∴2m+
=kπ,k∈Z,
∵m>0,
∴m的最小值为
,
故选B
| 3 |
| π |
| 3 |
向左平移m个单位得到g(x)=2sin[2(x+m)-
| π |
| 3 |
| π |
| 3 |
∴g(
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
∴2m+
| 2π |
| 3 |
∵m>0,
∴m的最小值为
| π |
| 6 |
故选B
点评:此题考查了两角和与差的正弦函数公式,以及三角函数的图象变换,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
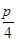 个单位,则所得到的图象对应的函数的一个单调递增区间是
个单位,则所得到的图象对应的函数的一个单调递增区间是 ) C.(
) C.(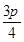 ) D.(
) D.(