题目内容
数列{an}的前项n和记为Sn,数列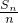 是首项为2,公比也为2 的等比数列.
是首项为2,公比也为2 的等比数列.
(Ⅰ)求an;
(Ⅱ)若数列 的前n项和不小于100,问此数列最少有多少项?
的前n项和不小于100,问此数列最少有多少项?
解:(Ⅰ)由题意,∵数列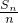 是首项为2,公比也为2 的等比数列.
是首项为2,公比也为2 的等比数列.
∴
∴Sn=n•2n
∴n≥2时,
当n=1时,结论也成立,
故
(Ⅱ)由(Ⅰ)知,
∴数列 的前n项和为
的前n项和为
∴
∴n≥19
即数列最少有19项.
分析:(Ⅰ)根据数列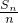 是首项为2,公比也为2 的等比数列,可求 Sn=n•2n,再写一式,相减可求an;
是首项为2,公比也为2 的等比数列,可求 Sn=n•2n,再写一式,相减可求an;
(Ⅱ) 先求数列 的前n项和,再建立不等式,即可求.
的前n项和,再建立不等式,即可求.
点评:本题以等比数列为载体,考查数列的通项,考查等差数列的前n项和,有一定的综合性.
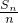 是首项为2,公比也为2 的等比数列.
是首项为2,公比也为2 的等比数列.∴

∴Sn=n•2n
∴n≥2时,

当n=1时,结论也成立,
故

(Ⅱ)由(Ⅰ)知,

∴数列
 的前n项和为
的前n项和为
∴

∴n≥19
即数列最少有19项.
分析:(Ⅰ)根据数列
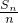 是首项为2,公比也为2 的等比数列,可求 Sn=n•2n,再写一式,相减可求an;
是首项为2,公比也为2 的等比数列,可求 Sn=n•2n,再写一式,相减可求an;(Ⅱ) 先求数列
 的前n项和,再建立不等式,即可求.
的前n项和,再建立不等式,即可求.点评:本题以等比数列为载体,考查数列的通项,考查等差数列的前n项和,有一定的综合性.

练习册系列答案
相关题目
数列an满足:a1=2,an+1=1-
,数列an的前项n积为
,则
( )
| 1 |
| an |
 |
| n |
 |
| 2010 |
A、-
| ||
| B、-1 | ||
C、
| ||
| D、1 |