题目内容
过双曲线 上任意一点P,引与实轴平行的直线,交两渐近线于M、N两点,则
上任意一点P,引与实轴平行的直线,交两渐近线于M、N两点,则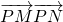 的值为
的值为
- A.a2
- B.b2
- C.2ab
- D.a2+b2
A
分析:本题考查的主要知识点是双曲线的性质中渐近线的性质,由双曲线的标准方程,我们不难线出双曲线的渐近线方程,又因为实轴平行的直线上各点的纵坐标相等,故设出P点坐标后,易给出M,N的坐标,进而给出对应向量的坐标,代入向量数量积坐标运算公式,即可求出答案.
解答:设p(x,y),则
 ,
,
于是 =
= .
.
故选A
点评:双曲线 (a>0,b>0)的渐近线方程是y=±
(a>0,b>0)的渐近线方程是y=± x,双曲线
x,双曲线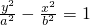 (a>0,b>0)的渐近线方程是y=±
(a>0,b>0)的渐近线方程是y=± x.
x.
分析:本题考查的主要知识点是双曲线的性质中渐近线的性质,由双曲线的标准方程,我们不难线出双曲线的渐近线方程,又因为实轴平行的直线上各点的纵坐标相等,故设出P点坐标后,易给出M,N的坐标,进而给出对应向量的坐标,代入向量数量积坐标运算公式,即可求出答案.
解答:设p(x,y),则
 ,
,于是
 =
= .
.故选A
点评:双曲线
 (a>0,b>0)的渐近线方程是y=±
(a>0,b>0)的渐近线方程是y=± x,双曲线
x,双曲线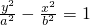 (a>0,b>0)的渐近线方程是y=±
(a>0,b>0)的渐近线方程是y=± x.
x. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 上任意一点P作x轴的平行线交两条渐近线于Q,R两点,则
上任意一点P作x轴的平行线交两条渐近线于Q,R两点,则 = .
= . 上任意一点P,引与实轴平行的直线,交两渐近线于M、N两点,则
上任意一点P,引与实轴平行的直线,交两渐近线于M、N两点,则 的值为( )
的值为( ) 上任意一点P,引与实轴平行的直线,交两渐近线于M、N两点,则
上任意一点P,引与实轴平行的直线,交两渐近线于M、N两点,则 = .
= . 上任意一点P,引与实轴平行的直线,交两渐近线于M、N两点,则
上任意一点P,引与实轴平行的直线,交两渐近线于M、N两点,则 的值为( )
的值为( )