题目内容
求证:在一个平面内,过直线l外一点P只能作出一条直线垂直于l.
证明:假设过点P可以作两条直线垂直于直线l,如图,那么∠PAB=90°,于是∠APB+∠PAB+∠PBA>180°,即△PAB的内角和大于180°,这与三角形内角和定理矛盾,故假设不成立.
所以,在一个平面内,过直线l外一点P只能作出一条直线垂直于l.绿色通道:
用反证法证明数学命题,需要注意以下几点:
(1)“否定结论”是反证法的第一步,它的正确与否直接影响能否正确使用反证法.否定结论的步骤是:①弄清结论本身的情况;②找出结论的全部相反情况;③正确否定上述结论.
(2)反证法中引出矛盾的结论,不是推理本身的错误,而是开始假定“结论的反面是正确的”是错误的.
(3)在反证法证题的过程中,经常画出某些不合常理的图形,甚至是不可能存在的图形,这样做的目的是为了能清楚地说明问题.在证明过程中,每一步推理所得结论的正确性,完全由它所依据的理由来保证,而不能借助图形的直观,这与用直接证法通过图形直接找到证题的途径是完全不一样的.
黑色陷阱:
用反证法证明命题时,若原命题问题的反面不唯一,这时容易漏掉一些情况,对于这种情形,要把每种可能一一否定,不要遗漏.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
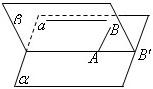 13、求证:若一直线与一个平面平行,则过平面内的一点且与这条直线平行的直线必在此平面内.
13、求证:若一直线与一个平面平行,则过平面内的一点且与这条直线平行的直线必在此平面内.