题目内容
已知
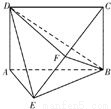
ABCD，ABEF是两个正方形，且不在一个平面内，M，N分别是对角线AC，FB上的点，且AM=FN．求证MN∥平面CBE．
答案：
解析：
解析：
|
证明：在 ABCD内，作 ∥AB交于BC于 ；
在 ABEF内，作NH∥AB交BE于H；连接 ．
因为  ∥AB，NH∥AB，所以 ∥NH．
又 ABCD，ABEF为全等的正方形，所以AC=BF．因为 AM=FN，所以CM=BN ，所以  ≌R t△BNH，所以=NH．
所以  NH．
所以  为平行四边形．
所以 MN∥ ．
又 MN 平面CBE， 平面CBE，所以MN∥平面CBE．
|
练习册系列答案
相关题目
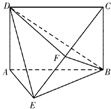已知?ABCD，直线BC⊥平面ABE，F为CE的中点．
已知ABCD是正方形，直线AE⊥平面ABCD，且AB=AE=1，
