题目内容
已知数列![]() 满足
满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)当![]() 时,证明不等式:
时,证明不等式:![]() .
.
(1)![]() .
.
(2)证明见解析
解析:
(1)当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,所以
,所以![]() .因此:
.因此:
当![]() 时,数列
时,数列![]() 是各项为0的常数列,所以
是各项为0的常数列,所以![]() .
.
当![]() 时,数列
时,数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,所以
为公比的等比数列,所以![]() ,所以
,所以![]() .又
.又![]() 适合此式,因此
适合此式,因此![]() .
.
综①②,得![]() .
.
(2)由![]() ,得
,得![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]()
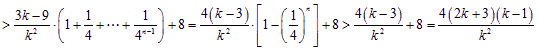 .
.
因为![]() ,所以
,所以![]() ,因此不等式
,因此不等式![]() 成立.
成立.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
题目内容
已知数列![]() 满足
满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)当![]() 时,证明不等式:
时,证明不等式:![]() .
.
(1)![]() .
.
(2)证明见解析
(1)当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,所以
,所以![]() .因此:
.因此:
当![]() 时,数列
时,数列![]() 是各项为0的常数列,所以
是各项为0的常数列,所以![]() .
.
当![]() 时,数列
时,数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,所以
为公比的等比数列,所以![]() ,所以
,所以![]() .又
.又![]() 适合此式,因此
适合此式,因此![]() .
.
综①②,得![]() .
.
(2)由![]() ,得
,得![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]()
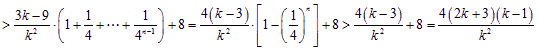 .
.
因为![]() ,所以
,所以![]() ,因此不等式
,因此不等式![]() 成立.
成立.

 金钥匙试卷系列答案
金钥匙试卷系列答案