题目内容
设{an}是首项为a,公差为d的等差数列(d≠0),Sn是其前n项和.
(Ⅰ) 若a2•a9=130,a4+a7=31,求数列{an}的通项公式;
(Ⅱ) 记bn=
,n∈N*,且b1,b2,b4成等比数列,证明:Snk=n2Sk(k,n∈N*).
(Ⅰ) 若a2•a9=130,a4+a7=31,求数列{an}的通项公式;
(Ⅱ) 记bn=
| Sn | n |
分析:(Ⅰ)a2+a9=a4+a7=31,知a2,a9是方程x2-31x+130=0的两个实数根,解出方程,利用等差数列的通项公式可得an;
(Ⅱ)表示出Sn,bn,由b1,b2,b4成等比数列,得a,d的关系式,从而可化简Sn,代入等式左右两边验证即可;
(Ⅱ)表示出Sn,bn,由b1,b2,b4成等比数列,得a,d的关系式,从而可化简Sn,代入等式左右两边验证即可;
解答:(Ⅰ)解:∵{an}是等差数列,由性质知a2+a9=a4+a7=31,
∴a2,a9是方程x2-31x+130=0的两个实数根,解得x1=5,x2=26,
当a2=5,a9=26时,d=3,an=3n-1;当a2=26,a9=5时,d=-3,an=-3n+32;
∴an=3n-1或an=-3n+32;
(Ⅱ)证明:由题意知Sn=na+
d,
∴bn=
=a+
d,
∵b1,b2,b4成等比数列,∴b22=b1b4,
∴(a+
d)2=a(a+
d),∴
ad-
d2=0,
∴
d(a-
d)=0,
∵d≠0,∴a=
d,∴d=2a,
∴Sn=na+
d=na+
2a=n2a,
∴左边=Snk=(nk)2a=n2k2a,右边=n2Sk=n2k2a,∴左边=右边,
∴Snk=n2Sk(k,n∈N*)成立.
∴a2,a9是方程x2-31x+130=0的两个实数根,解得x1=5,x2=26,
当a2=5,a9=26时,d=3,an=3n-1;当a2=26,a9=5时,d=-3,an=-3n+32;
∴an=3n-1或an=-3n+32;
(Ⅱ)证明:由题意知Sn=na+
| n(n-1) |
| 2 |
∴bn=
| Sn |
| n |
| n-1 |
| 2 |
∵b1,b2,b4成等比数列,∴b22=b1b4,
∴(a+
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
∵d≠0,∴a=
| 1 |
| 2 |
∴Sn=na+
| n(n-1) |
| 2 |
| n(n-1) |
| 2 |
∴左边=Snk=(nk)2a=n2k2a,右边=n2Sk=n2k2a,∴左边=右边,
∴Snk=n2Sk(k,n∈N*)成立.
点评:本题考查了等差数列和等比数列的性质,考查了等差数列的前n项和,考查了学生的运算能力,解答此题的关键是理解并掌握非常数等差数列的通项公式是关于n的一次函数,此题是中档题.

练习册系列答案
相关题目
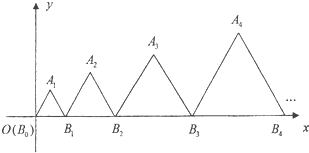 如图,在平面直角坐标系中,边长为an的一组正三角形AnBn-1Bn的底边Bn-1Bn依次排列在x轴上(B0与坐标原点重合).设{an}是首项为a,公差为d的等差数列,若所有正三角形顶点An在第一象限,且均落在抛物线y2=2px(p>0)上,则
如图,在平面直角坐标系中,边长为an的一组正三角形AnBn-1Bn的底边Bn-1Bn依次排列在x轴上(B0与坐标原点重合).设{an}是首项为a,公差为d的等差数列,若所有正三角形顶点An在第一象限,且均落在抛物线y2=2px(p>0)上,则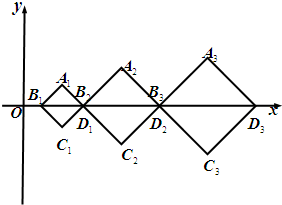 (2009•上海)如图,在直角坐标系xOy中,有一组对角线长为an的正方形AnBnCnDn(n=1,2,…),其对角线BnDn依次放置在x轴上(相邻顶点重合).设{an}是首项为a,公差为d(d>0)的等差数列,点B1的坐标为(d,0).
(2009•上海)如图,在直角坐标系xOy中,有一组对角线长为an的正方形AnBnCnDn(n=1,2,…),其对角线BnDn依次放置在x轴上(相邻顶点重合).设{an}是首项为a,公差为d(d>0)的等差数列,点B1的坐标为(d,0). 的值为( )
的值为( )


