题目内容
5．过点O（0，0）作直线与圆（x-4$\sqrt{5}$）2+（y-8）2=169相交，则在弦长为整数的所有直线中，等可能的任取一条直线，则弦长长度不超过14的概率为（ ）| A． | $\frac{9}{10}$ | B． | $\frac{15}{32}$ | C． | $\frac{9}{32}$ | D． | $\frac{7}{32}$ |
分析 利用圆的标准方程求出圆的圆心及半径，求出当直线与圆心和（0，0）连线垂直时的弦长即最短的弦长，求出直径即最大的弦长，求出最大弦长与最小弦长之间的所有的直线条数，选出长度不超过14的直线条数，利用古典概型概率公式求出概率．
解答 解：（x-4$\sqrt{5}$）2+（y-8）2=169的圆心为（4$\sqrt{5}$，8），半径为13，
∵（0，0）在圆的内部且圆心与（0，0）的距离为12
∴过点O（0，0）作的直线中，最短的弦是直线与圆心和（0，0）连线垂直
最短的弦长为2$\sqrt{169-144}$=10，
过点O（0，0）作的直线中，最长的弦是直径，其长为26
弦长均为整数的所有直线的条数有2×（25-10）+2=32
其中长度不超过14的有：10，11，11，12，12，13，13，14，14共9条
所以长度不超过14的概率为$\frac{9}{32}$．
故选C．
点评 求直线的最小弦长、最大弦长问题一般利用圆的几何性质：当直线与定点和圆心连线垂直时，弦长最小，当直线是圆的直径时，弦长最大．
练习册系列答案
相关题目
13．已知tanα=-$\frac{3}{4}$，且α∈（0，π），则cosα=（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{1}{2}$ | C． | -$\frac{4}{5}$ | D． | $\frac{3}{5}$ |
20．在△ABC中，∠A=60°，AC=3，面积为$\frac{{3\sqrt{3}}}{2}$，那么BC的长度为（ ）
| A． | $\sqrt{7}$ | B． | 3 | C． | 2$\sqrt{2}$ | D． | $\sqrt{13}$ |
10．已知定义在R上的可导函数f（x）的导函数为f'（x），满足f'（x）＜f（x），且f（x+3）为偶函数，f（6）=1，则不等式f（x）＞ex的解集为（ ）
| A． | （-∞，0） | B． | （0，+∞） | C． | （1，+∞） | D． | （4，+∞） |
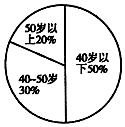200名职工年龄分布如图所示，从中随机抽取40名职工作样本，采用系统抽样方式，按1～200编号分为40组，分别为1～5，6～10，…，196～200，第5组抽取号码为23，第9组抽取号码为43；若采用分层抽样，40-50岁年龄段应抽取12人．