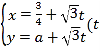题目内容
【题目】已知点![]() 在椭圆
在椭圆![]() :
:![]() (
(![]() )上,且点
)上,且点![]() 到左焦点
到左焦点![]() 的距离为3.
的距离为3.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 关于坐标原点
关于坐标原点![]() 的对称点为
的对称点为![]() ,又
,又![]()
![]() 两点在椭圆
两点在椭圆![]() 上,且
上,且![]() ,求凸四边形
,求凸四边形![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由题意点![]() 到左焦点
到左焦点![]() 的距离为3,结合两点间距离公式可求得
的距离为3,结合两点间距离公式可求得![]() 的值,将点
的值,将点![]() 代入椭圆,根据椭圆中
代入椭圆,根据椭圆中![]() 的关系式即可求得
的关系式即可求得![]() ,进而得椭圆的标准方程.
,进而得椭圆的标准方程.
(2)由![]() 可设直线
可设直线![]() 的方程为
的方程为![]() ,联立椭圆方程,整理变形根据两个交点可令
,联立椭圆方程,整理变形根据两个交点可令![]() 求得
求得![]() 的范围.设
的范围.设![]()
![]() ,由韦达定理表示出
,由韦达定理表示出![]() ,
,![]() ,由弦长公式求得
,由弦长公式求得![]() ,点到直线距离公式求得
,点到直线距离公式求得![]() 到
到![]() 的距离,结合
的距离,结合![]() 用
用![]() 表示出
表示出![]() ,令
,令![]() ,可化简为
,可化简为![]() ,再令
,再令![]() ,利用导函数求得
,利用导函数求得![]() 的单调性和最值,即可求解.
的单调性和最值,即可求解.
(1)因为椭圆![]() 经过点
经过点![]() ,所以
,所以![]() .
.
设左焦点![]() (
(![]() ),
),
则由![]() 得
得![]() ,
,
解得![]() .
.
又![]() ,于是
,于是![]() ,
,
解得![]() (舍负),
(舍负),
进而![]() .
.
故椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)因为![]() ,可设直线
,可设直线![]() 的方程为
的方程为![]() (
(![]() ),
),
联立 并整理得
并整理得![]() .
.
由![]() ,解得
,解得![]() .
.
设![]()
![]() ,则
,则![]() ,
,![]() .
.
所以![]()
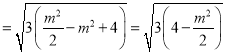 .
.
又![]() 与
与![]() 之间的距离即
之间的距离即![]() 到
到![]() 的距离
的距离![]() ,且
,且![]() .
.
所以四边形![]() 的面积
的面积 .
.
设![]() ,由
,由![]() 可得
可得![]() ,
,
则![]() ,
,
记之为函数![]() ,则
,则![]() ,
,
易知![]() 在区间
在区间![]() 内单调递增,在区间
内单调递增,在区间![]() 内单调递减.
内单调递减.
故![]() 的最大值为
的最大值为![]() ,此时
,此时![]() ,解得
,解得![]() ,符合题意,
,符合题意,
所以四边形![]() 面积的最大值为
面积的最大值为![]() .
.

【题目】某家庭记录了未使用节水龙头50天的日用水量数据(单位:![]() )和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用水量 | [0,0.1) | [0.1,0.2) | [0.2,0.3) | [0.3,0.4) | [0.4,0.5) | [0.5,0.6) | [0.6,0.7) |
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 | [0,0.1) | [0.1,0.2) | [0.2,0.3) | [0.3,0.4) | [0.4,0.5) | [0.5,0.6) |
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)作出使用了节水龙头50天的日用水量数据的频率分布直方图;
(2)估计该家庭使用节水龙头后,日用水量小于0.3![]() 的概率;
的概率;
(3)估计该家庭用节水龙头后,一年能节省多少水.(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表)