题目内容
两非零向量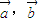 满足:2
满足:2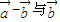 垂直,集合A={x|x2+(|
垂直,集合A={x|x2+(|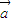 |+|
|+|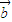 |)x+|
|)x+|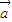 ||
||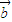 |=0}是单元素集合.
|=0}是单元素集合.(1)求
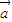 与
与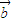 的夹角
的夹角(2)若关于t的不等式|
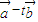 |<|
|<|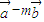 |的解集为空集,求实数m的值.
|的解集为空集,求实数m的值.
【答案】分析:(1)由题意可得 ,
, ,代入夹角公式可得答案;
,代入夹角公式可得答案;
(2)由(1)可把不等式转化为:t2-t+m-m2≥0对一切t∈R恒成立,可得△=1-4(m-m2)≤0,解之即可.
解答:解:(1)由2 垂直得
垂直得 =0,即
=0,即 ,
,
由A={x|x2+(| |+|
|+| |)x+|
|)x+| ||
|| |=0}是单元素集合得:
|=0}是单元素集合得:
△= ,即
,即 ,
,
设 与
与 的夹角为θ,由夹角公式可得cosθ=
的夹角为θ,由夹角公式可得cosθ= =
= =
= ,
,
故θ= ,故
,故 与
与 的夹角为
的夹角为
(2)关于t的不等式| |<|
|<| |的解集为空集,则
|的解集为空集,则
不等式| |≥|
|≥| |的解集为R,
|的解集为R,
从而 ≥
≥ 对一切t∈R恒成立,
对一切t∈R恒成立,
将 ,
, 代入上式得:t2-t+m-m2≥0对一切t∈R恒成立,
代入上式得:t2-t+m-m2≥0对一切t∈R恒成立,
∴△=1-4(m-m2)≤0,即(2m-1)2≤0,解得m=
点评:本题为向量的综合应用,涉及夹角公式和不等式的恒成立问题,属中档题.
 ,
, ,代入夹角公式可得答案;
,代入夹角公式可得答案;(2)由(1)可把不等式转化为:t2-t+m-m2≥0对一切t∈R恒成立,可得△=1-4(m-m2)≤0,解之即可.
解答:解:(1)由2
 垂直得
垂直得 =0,即
=0,即 ,
,由A={x|x2+(|
 |+|
|+| |)x+|
|)x+| ||
|| |=0}是单元素集合得:
|=0}是单元素集合得:△=
 ,即
,即 ,
,设
 与
与 的夹角为θ,由夹角公式可得cosθ=
的夹角为θ,由夹角公式可得cosθ= =
= =
= ,
,故θ=
 ,故
,故 与
与 的夹角为
的夹角为
(2)关于t的不等式|
 |<|
|<| |的解集为空集,则
|的解集为空集,则不等式|
 |≥|
|≥| |的解集为R,
|的解集为R,从而
 ≥
≥ 对一切t∈R恒成立,
对一切t∈R恒成立,将
 ,
, 代入上式得:t2-t+m-m2≥0对一切t∈R恒成立,
代入上式得:t2-t+m-m2≥0对一切t∈R恒成立,∴△=1-4(m-m2)≤0,即(2m-1)2≤0,解得m=

点评:本题为向量的综合应用,涉及夹角公式和不等式的恒成立问题,属中档题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
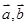 满足:
满足: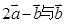 垂直,集合
垂直,集合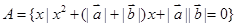 是单元素集合。
是单元素集合。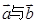 的夹角;
的夹角;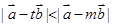 的解集为空集,求实数m的值。
的解集为空集,求实数m的值。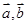 满足:
满足: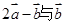 垂直,集合
垂直,集合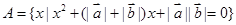 是单元素集合。
是单元素集合。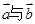 的夹角;
的夹角;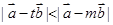 的解集为空集,求实数m的值。
的解集为空集,求实数m的值。 满足:2
满足:2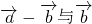 垂直,集合A={x|x2+(|
垂直,集合A={x|x2+(| |+|
|+| |)x+|
|)x+|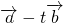 |<|
|<|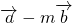 |的解集为空集,求实数m的值.
|的解集为空集,求实数m的值.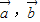 满足:2
满足:2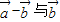 垂直,集合A={x|x2+(|
垂直,集合A={x|x2+(|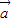 |+|
|+|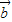 |)x+|
|)x+| ||
|| |=0}是单元素集合.
|=0}是单元素集合.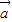 与
与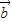 的夹角
的夹角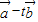 |<|
|<|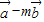 |的解集为空集,求实数m的值.
|的解集为空集,求实数m的值.