题目内容
已知椭圆 的离心率为
的离心率为 ,直线y=
,直线y=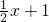 与椭圆相交于A、B两点,点M在椭圆上,且满足
与椭圆相交于A、B两点,点M在椭圆上,且满足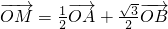 .则b=________.
.则b=________.
1
分析:先根据离心率求得a和b的关系,进而设出椭圆方程,将直线与椭圆方程联立消去y,求得交点的横坐标,进而根据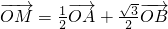 分别表示出M的横坐标和纵坐标,代入椭圆方程后化简整理即可求得b.
分别表示出M的横坐标和纵坐标,代入椭圆方程后化简整理即可求得b.
解答:∵由e=
∴a=2b;
设椭圆方程为
将直线方程与椭圆方程联立得
消去y得:x2+2x+2-2b2=0
则x1=-1+ ,x2=-1-
,x2=-1- ,
,
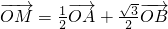 =(
=(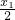 +
+ ,
, +
+ )
)
∴xM=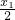 +
+ =-
=- +(1-
+(1- )
)
yM= +
+ =
= +
+
∵M在椭圆上,
代入椭圆方程得xM2+(1+ )xM+1+
)xM+1+ -2b2=0
-2b2=0
求得b2=1,b=1
故答案为:1
点评:本题主要考查了椭圆的简单性质.考查了学生综合分析问题和解决问题的能力.
分析:先根据离心率求得a和b的关系,进而设出椭圆方程,将直线与椭圆方程联立消去y,求得交点的横坐标,进而根据
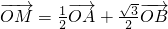 分别表示出M的横坐标和纵坐标,代入椭圆方程后化简整理即可求得b.
分别表示出M的横坐标和纵坐标,代入椭圆方程后化简整理即可求得b.解答:∵由e=

∴a=2b;
设椭圆方程为

将直线方程与椭圆方程联立得
消去y得:x2+2x+2-2b2=0
则x1=-1+
 ,x2=-1-
,x2=-1- ,
,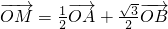 =(
=(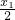 +
+ ,
, +
+ )
) ∴xM=
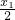 +
+ =-
=- +(1-
+(1- )
)
yM=
 +
+ =
= +
+
∵M在椭圆上,
代入椭圆方程得xM2+(1+
 )xM+1+
)xM+1+ -2b2=0
-2b2=0求得b2=1,b=1
故答案为:1
点评:本题主要考查了椭圆的简单性质.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
已知椭圆的离心率为e,两焦点分别为F1、F2,抛物线C以F1为顶点、F2为焦点,点P为抛物线和椭圆的一个交点,若e|PF2|=|PF1|,则e的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
已知椭圆的离心率为
,焦点是(-3,0),(3,0),则椭圆方程为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: 如图,A,B是椭圆C:
如图,A,B是椭圆C: