题目内容
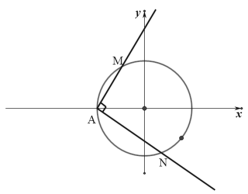
【题目】![]() 是双曲线
是双曲线![]() 的左右焦点,过
的左右焦点,过![]() 且斜率为1的直线与两条渐近线分别交于
且斜率为1的直线与两条渐近线分别交于![]() 两点,若
两点,若![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】设直线方程为![]() ,与渐近线方程
,与渐近线方程![]() 联立方程组解得
联立方程组解得![]() 因为
因为![]() ,所以
,所以![]()
![]() ,选B.
,选B.
点睛:解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于![]() 的方程或不等式,再根据
的方程或不等式,再根据![]() 的关系消掉
的关系消掉![]() 得到
得到![]() 的关系式,而建立关于
的关系式,而建立关于![]() 的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.
的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.
【题型】单选题
【结束】
10
【题目】设![]() 是两条不同的直线,
是两条不同的直线, ![]() 是两个不同的平面,则下列命题中正确的是( )
是两个不同的平面,则下列命题中正确的是( )
A. 若![]() ,
, ![]() ,则
,则![]()
B. 若![]() ,
, ![]() ,则
,则![]()
C. 若![]() ,
, ![]() ,
, ![]() ,则
,则![]()
D. 若![]() ,且
,且![]() ,点
,点![]() ,直线
,直线![]() ,则
,则![]()
【答案】C
【解析】A. 若![]() ,
, ![]() ,则
,则![]() 或
或![]() ;
;
B. 若![]() ,
, ![]() ,则
,则![]() 无交点,即平行或异面;
无交点,即平行或异面;
C. 若![]() ,
, ![]() ,
, ![]() ,过
,过![]() 作平面与
作平面与![]() 分别交于直线s,t,则
分别交于直线s,t,则![]() ,
, ![]() ,所以
,所以![]() t,再根据线面平行判定定理得
t,再根据线面平行判定定理得![]() ,因为
,因为![]() ,
, ![]() ,所以
,所以![]() ,即
,即![]()
D. 若![]() ,且
,且![]() ,点
,点![]() ,直线
,直线![]() ,当B在平面
,当B在平面![]() 内时才有
内时才有![]() ,
,
综上选C.

练习册系列答案
相关题目