题目内容
若数列{an}满足
-
=d,(n∈N*,d为常数),则称数列{an}为调和数列.已知数列{
}为调和数列,且x1+x2+x3+…+x20=200,则x1+x20=______;x3x18的最大值等于______.
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| xn |
因为数列{
}为调和数列,
所以结合调和数列的定义可得:xn+1-xn=d=常数,
所以数列{xn}是等差数列.
因为x1+x2+x3+…+x20=200,
所以结合等差数列的性质可得:x1+x2+x3+…+x20=10(x1+x20)=200,
所以x1+x20=20,
所以20=x3+x18≥2
,即x3x18≤100.
故答案为20,100.
| 1 |
| xn |
所以结合调和数列的定义可得:xn+1-xn=d=常数,
所以数列{xn}是等差数列.
因为x1+x2+x3+…+x20=200,
所以结合等差数列的性质可得:x1+x2+x3+…+x20=10(x1+x20)=200,
所以x1+x20=20,
所以20=x3+x18≥2
| x3x18 |
故答案为20,100.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
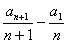 =1,且
=1,且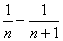 =2(n∈N*),则a10为( )
=2(n∈N*),则a10为( ) =1,且
=1,且 =2(n∈N*),则a3=____________,数列{an}的通项公式为an=____________.
=2(n∈N*),则a3=____________,数列{an}的通项公式为an=____________. =ad-bc,若数列{an}满足
=ad-bc,若数列{an}满足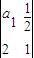 =1,且
=1,且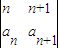 =2(n∈N*)则a3= .数列{an}的通项公式为an= .
=2(n∈N*)则a3= .数列{an}的通项公式为an= . =ad-bc,若数列{an}满足
=ad-bc,若数列{an}满足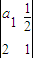 =1,且
=1,且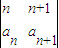 =2(n∈N*)则a3= .数列{an}的通项公式为an= .
=2(n∈N*)则a3= .数列{an}的通项公式为an= .