题目内容
如图,正三棱柱![]() 的所有棱长都为
的所有棱长都为![]() ,
,![]() 为
为![]() 中点.
中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求点![]() 到平面
到平面![]() 的距离。
的距离。

解:(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]() .
.
![]() 为正三角形,
为正三角形,![]() .
.
![]() 正三棱柱
正三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]()
连结![]() ,在正方形
,在正方形![]() 中,
中,![]() 分别为
分别为![]() 的中点,
的中点,
![]() ,
,
![]() .
.
(方法二:利用等腰三角形![]() 证明
证明![]() 的相应给分,H为AB1与A1B的交点)
的相应给分,H为AB1与A1B的交点)
在正方形![]() 中,
中,![]() ,
,
![]() 平面
平面![]() .
.
(2)运用等积法求解,![]() 中,
中,![]() ,
,
![]() 同理
同理![]() .
.
作![]() ,则E为
,则E为![]() 的中点,∴DE=2.
的中点,∴DE=2.
![]()
由(1) ![]() 平面
平面![]() ,且
,且![]()
∴![]() 到面
到面![]() 的距离为
的距离为![]() , 设点B到面
, 设点B到面![]() 的距离为h,
的距离为h,
由![]() 得
得![]()
![]() , 求得h=
, 求得h=![]() .∴点B到面
.∴点B到面![]() 的距离为
的距离为![]() 。
。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
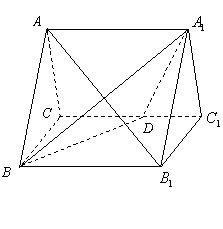
 (本题满分10分)
(本题满分10分) 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。 ∥平面
∥平面 ;
; 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

 的所有棱长都为2,
的所有棱长都为2, 为
为 中点
中点 (1)求证:
(1)求证: 平面
平面
 的大小
的大小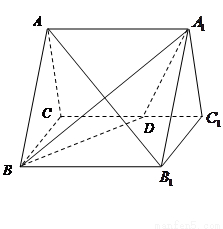 如图,正三棱柱
如图,正三棱柱 的所有棱长都为
的所有棱长都为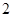 ,
,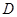 为
为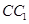 中点.
中点.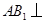 平面
平面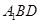 ;
;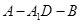 的大小;
的大小; 到平面
到平面