题目内容
【题目】已知一组数据x1 , x2 , x3 , x4 , x5的平均数是2,方差是 ![]() ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣3,3x4﹣2,3x5﹣2的平均数和方差分别为( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣3,3x4﹣2,3x5﹣2的平均数和方差分别为( )
A.2, ![]()
B.4,3
C.4, ![]()
D.2,1
【答案】B
【解析】解:∵x1 , x2 , …,x5的平均数是2,则x1+x2+…+x5=2×5=10.
∴数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数是: ![]() ′=
′= ![]() [(3x1﹣2)+(3x2﹣2)+(3x3﹣2)+(3x4﹣2)+(3x5﹣2)]=
[(3x1﹣2)+(3x2﹣2)+(3x3﹣2)+(3x4﹣2)+(3x5﹣2)]= ![]() [3×(x1+x2+…+x5)﹣10]=4,
[3×(x1+x2+…+x5)﹣10]=4,
S′2= ![]() ×[(3x1﹣2﹣4)2+(3x2﹣2﹣4)2+…+(3x5﹣2﹣4)2],
×[(3x1﹣2﹣4)2+(3x2﹣2﹣4)2+…+(3x5﹣2﹣4)2],
= ![]() ×[(3x1﹣6)2+…+(3x5﹣6)2]=9×
×[(3x1﹣6)2+…+(3x5﹣6)2]=9× ![]() [(x1﹣2)2+(x2﹣2)2+…+(x5﹣2)2]=3.
[(x1﹣2)2+(x2﹣2)2+…+(x5﹣2)2]=3.
故选B.
【考点精析】解答此题的关键在于理解平均数、中位数、众数的相关知识,掌握⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据,以及对极差、方差与标准差的理解,了解标准差和方差越大,数据的离散程度越大;标准差和方程为0时,样本各数据全相等,数据没有离散性;方差与原始数据单位不同,解决实际问题时,多采用标准差.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】电视传媒公司为了解某地区观众对某体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”. 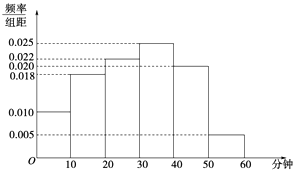
(1)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(2)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为X.若每次抽取的结果是相互独立的,求X的分布列,期望E(X)和方差D(X).
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
附:K2= ![]() .
.