题目内容
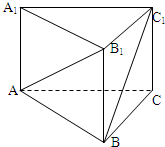如图，正三棱柱ABC-A1B1C1的所有棱的长度都为4，则异面直线AB1与BC1所成的角是分析：利用两个向量数量积的定义求得
•
，由
•
=（
+
）•（
+
）求得
•
，求得cos＜
，
＞=
，故异面直线AB1与BC1所成的角是arccos
．
| AB1 |
| BC1 |
| AB1 |
| BC1 |
| AB |
| BB1 |
| BC |
| CC1 |
| AB1 |
| BC1 |
| AB1 |
| BC1 |
| 1 |
| 4 |
| 1 |
| 4 |
解答：解：
•
=4
×4
cos＜
，
＞=32cos＜
＞．
又
•
=（
+
）•（
+
）=
•
+
•
+
•
+
•
=4×4cos120°+0+0+4×4=8．
故有 32cos＜
，
＞=8，∴cos＜
，
＞=
，∴＜
，
＞=arccos
，
故异面直线AB1与BC1所成的角是 arccos
，
故答案为arccos
．
| AB1 |
| BC1 |
| 2 |
| 2 |
| AB1 |
| BC1 |
| AB1 |
| ， BC1 |
又
| AB1 |
| BC1 |
| AB |
| BB1 |
| BC |
| CC1 |
| AB |
| BC |
| AB |
| CC1 |
| BB1 |
| BC |
| BB1 |
| CC1 |
=4×4cos120°+0+0+4×4=8．
故有 32cos＜
| AB1 |
| BC1 |
| AB1 |
| BC1 |
| 1 |
| 4 |
| AB1 |
| BC1 |
| 1 |
| 4 |
故异面直线AB1与BC1所成的角是 arccos
| 1 |
| 4 |
故答案为arccos
| 1 |
| 4 |
点评：本题考查异面直线所成的角的定义和求法，体现了转化的数学思想，求出cos＜
，
＞的值，是解题的关键．
| AB1 |
| BC1 |
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
如图，正三棱柱ABC-A1B1C1各棱长都等于a，E是BB1的中点．
如图，正三棱柱ABC-A1B1C1的各棱长都2，E，F分别是AB，A1C1的中点，则EF的长是（ ）| A、2 | ||
B、
| ||
C、
| ||
D、
|
如图，正三棱柱ABC-A1B1C1的所有棱长都为2，D为CC1中点．
（2013•郑州二模）如图，正三棱柱ABC-A1B1C1的所有棱长都为2，D为CC1中点．
如图，正三棱柱ABC-A1B1C1中（注：底面为正三角形且侧棱与底面垂直），BC=CC1=2，P，Q分别为BB1，CC1的中点．