题目内容
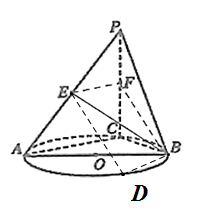
【题目】如图,![]() 是圆
是圆![]() 的直径,点
的直径,点![]() 是圆
是圆![]() 上异于
上异于![]() ,
,![]() 的点,直线
的点,直线![]() 平面
平面![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
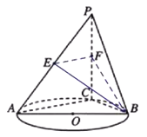
(Ⅰ)记平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,试判断直线
,试判断直线![]() 与平面
与平面![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(Ⅱ)设![]() ,求二面角
,求二面角![]() 大小的取值范围.
大小的取值范围.
【答案】(Ⅰ)![]() 平面
平面![]() ,证明见解析;(Ⅱ)
,证明见解析;(Ⅱ)![]()
【解析】
(Ⅰ)证出![]() 平面
平面![]() ,由线面平行的性质定理可证出
,由线面平行的性质定理可证出![]() ,再由线面平行的判定定理即可求解.
,再由线面平行的判定定理即可求解.
(Ⅱ)法一:证出![]() 是二面角
是二面角![]() 的平面角,
的平面角,![]() ,根据
,根据![]() 的范围即可求解.
的范围即可求解.
法二:以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立空间直角坐标系,求出平面
轴建立空间直角坐标系,求出平面![]() 的法向量与平面
的法向量与平面![]() 的法向量,利用向量的数量积即可求解.
的法向量,利用向量的数量积即可求解.
(Ⅰ)证明如下:
∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,平面
,平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,
,
∴![]() .
.
而![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)解法一:设直线![]() 与圆
与圆![]() 的另一个交点为
的另一个交点为![]() ,连结
,连结![]() ,
,![]() .
.
由(Ⅰ)知,![]() ,而
,而![]() ,∴
,∴![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
而![]() ,∴
,∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
∴![]() 是二面角
是二面角![]() 的平面角.
的平面角.
![]() .
.
注意到![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,
,
即二面角![]() 的取值范围是
的取值范围是![]() .
.
解法二:由题意,![]() ,以
,以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
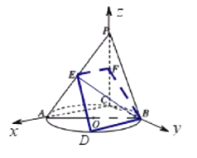
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则由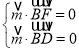 得
得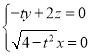 ,取
,取![]() 得
得![]() .
.
易知平面![]() 的法向量
的法向量![]() ,
,
设二面角![]() 的大小为
的大小为![]() ,易知
,易知![]() 为锐角,
为锐角,
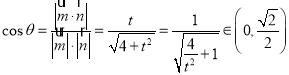 ,
,
∴![]() ,
,
即二面角![]() 的取值范围是
的取值范围是![]() .
.

【题目】近几年一种新奇水果深受广大消费者的喜爱,一位农户发挥聪明才智,把这种露天种植的新奇水果搬到了大棚里,收到了很好的经济效益.根据资料显示,产出的新奇水果的箱数x(单位:十箱)与成本y(单位:千元)的关系如下:
x | 1 | 3 | 4 | 6 | 7 |
y | 5 | 6.5 | 7 | 7.5 | 8 |
y与x可用回归方程![]() ( 其中
( 其中![]() ,
,![]() 为常数)进行模拟.
为常数)进行模拟.
(Ⅰ)若该农户产出的该新奇水果的价格为150元/箱,试预测该新奇水果100箱的利润是多少元.|.
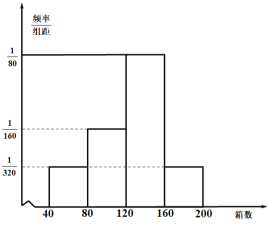
(Ⅱ)据统计,10月份的连续16天中该农户每天为甲地配送的该新奇水果的箱数的频率分布直方图如图所示.
(i)若从箱数在![]() 内的天数中随机抽取2天,估计恰有1天的水果箱数在
内的天数中随机抽取2天,估计恰有1天的水果箱数在![]() 内的概率;
内的概率;
(ⅱ)求这16天该农户每天为甲地配送的该新奇水果的箱数的平均值.(每组用该组区间的中点值作代表)
参考数据与公式:设![]() ,则
,则
|
|
|
|
0.54 | 6.8 | 1.53 | 0.45 |
线性回归直线![]() 中,
中, ,
,![]() .
.