题目内容
已知向量 ,记函数f(x)=
,记函数f(x)= ,
,若函数f(x)的最小正周期为π.
(1)求ω的值;
(2)当0<x≤
 时,试求f(x)的值域;
时,试求f(x)的值域;(3)求f(x)在[0,π]上的单调递增区间.
【答案】分析:(1)可利用向量的坐标运算公式结合正弦与余弦的二倍角公式求得f(x)=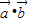 =sin(2ωx+
=sin(2ωx+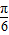 )+
)+ ,由最小正周期为π即可求得ω的值;
,由最小正周期为π即可求得ω的值;
(2)0<x≤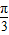 ⇒2x+
⇒2x+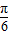 ∈(
∈(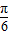 ,
,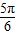 )⇒
)⇒ ≤sin(2x+
≤sin(2x+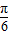 )≤1,f(x)的值域可求得;
)≤1,f(x)的值域可求得;
(3)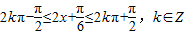 ⇒
⇒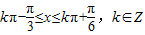 ,令k取特值0,1即可求得f(x)在[0,π]上的单调递增区间.
,令k取特值0,1即可求得f(x)在[0,π]上的单调递增区间.
解答:解:(1)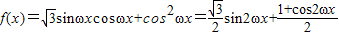 =
=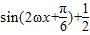 …(3分)
…(3分)
∵ω>0,∴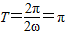 ,∴ω=1…(4分)
,∴ω=1…(4分)
(2)由(1),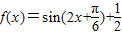 ,
,
∵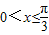 ,
,
∴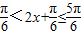 ,
,
∴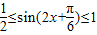 ,
,
∴f(x)的值域为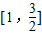 …(8分)
…(8分)
(3)由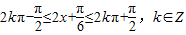 ,
,
得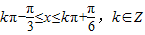 …(10分)
…(10分)
又∵x∈[0,π],∴ ,或
,或 ,
,
∴f(x)在[0,π]上的单调递增区间为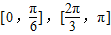 …(12分)
…(12分)
点评:本题考查平面向量数量积的运算,正弦函数的定义域和值域及正弦函数的单调性,着重考查正弦函数的图象与性质的综合应用,属于中档题.
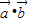 =sin(2ωx+
=sin(2ωx+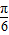 )+
)+ ,由最小正周期为π即可求得ω的值;
,由最小正周期为π即可求得ω的值;(2)0<x≤
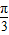 ⇒2x+
⇒2x+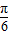 ∈(
∈(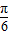 ,
,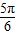 )⇒
)⇒ ≤sin(2x+
≤sin(2x+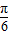 )≤1,f(x)的值域可求得;
)≤1,f(x)的值域可求得;(3)
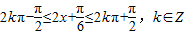 ⇒
⇒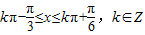 ,令k取特值0,1即可求得f(x)在[0,π]上的单调递增区间.
,令k取特值0,1即可求得f(x)在[0,π]上的单调递增区间.解答:解:(1)
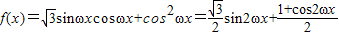 =
=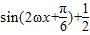 …(3分)
…(3分)∵ω>0,∴
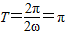 ,∴ω=1…(4分)
,∴ω=1…(4分)(2)由(1),
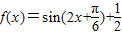 ,
,∵
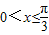 ,
,∴
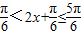 ,
,∴
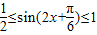 ,
,∴f(x)的值域为
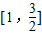 …(8分)
…(8分)(3)由
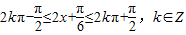 ,
,得
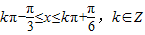 …(10分)
…(10分)又∵x∈[0,π],∴
 ,或
,或 ,
,∴f(x)在[0,π]上的单调递增区间为
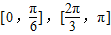 …(12分)
…(12分)点评:本题考查平面向量数量积的运算,正弦函数的定义域和值域及正弦函数的单调性,着重考查正弦函数的图象与性质的综合应用,属于中档题.

练习册系列答案
相关题目
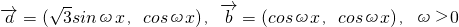 ,记函数f(x)=
,记函数f(x)= ,
, 时,试求f(x)的值域;
时,试求f(x)的值域;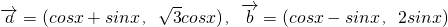 ,记
,记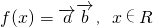 .
. ,记函数f(x)=
,记函数f(x)=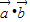 ,
, 时,试求f(x)的值域;
时,试求f(x)的值域;