题目内容
已知圆 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 ,点
,点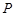 在直线
在直线 上,过
上,过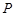 点作圆
点作圆 的切线
的切线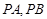 ,切点为
,切点为 .
.
(1)若 ,试求点
,试求点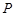 的坐标;
的坐标;
(2)求证:经过 三点的圆必过定点,并求出所有定点的坐标;
三点的圆必过定点,并求出所有定点的坐标;
(3)求弦 长的最小值.
长的最小值.
 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 ,点
,点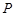 在直线
在直线 上,过
上,过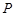 点作圆
点作圆 的切线
的切线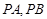 ,切点为
,切点为 .
.(1)若
 ,试求点
,试求点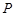 的坐标;
的坐标;(2)求证:经过
 三点的圆必过定点,并求出所有定点的坐标;
三点的圆必过定点,并求出所有定点的坐标;(3)求弦
 长的最小值.
长的最小值.(1)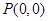 或
或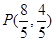 ;(2)见解析;(3)
;(2)见解析;(3)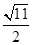 .
.
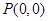 或
或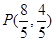 ;(2)见解析;(3)
;(2)见解析;(3)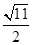 .
.(1)根据 ,求得
,求得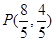 ;(2)求出圆的方程
;(2)求出圆的方程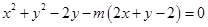 ,此式是关于
,此式是关于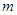 的恒等式,列条件;(3)表示出弦长,求最值。
的恒等式,列条件;(3)表示出弦长,求最值。
解:(1)设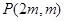 ,由题可知
,由题可知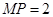 ,所以
,所以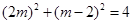 ,解之得:
,解之得: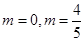 故所求点
故所求点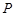 的坐标为
的坐标为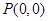 或
或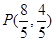 . ........4分
. ........4分
(2)设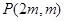 ,
, 的中点
的中点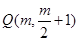 ,因为
,因为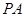 是圆
是圆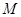 的切线
的切线
所以经过 三点的圆是以
三点的圆是以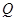 为圆心,以
为圆心,以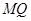 为半径的圆,
为半径的圆,
故其方程为: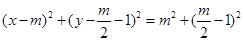 ........6分
........6分
化简得: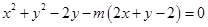 ,此式是关于
,此式是关于 的恒等式,
的恒等式,
故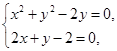 解得
解得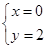 或
或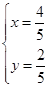
所以经过 三点的圆必过定点
三点的圆必过定点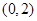 或
或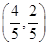 . ........10分
. ........10分
(3)设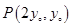 ,且
,且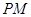 与
与 交于点
交于点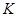 ,则
,则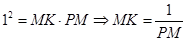
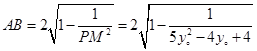 当
当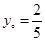 时,
时, 最小值为
最小值为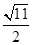 ...16分
...16分
(几何方法酌情给分)
 ,求得
,求得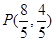 ;(2)求出圆的方程
;(2)求出圆的方程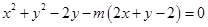 ,此式是关于
,此式是关于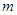 的恒等式,列条件;(3)表示出弦长,求最值。
的恒等式,列条件;(3)表示出弦长,求最值。解:(1)设
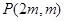 ,由题可知
,由题可知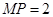 ,所以
,所以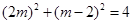 ,解之得:
,解之得: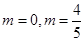 故所求点
故所求点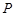 的坐标为
的坐标为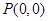 或
或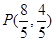 . ........4分
. ........4分 (2)设
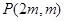 ,
,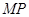 的中点
的中点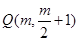 ,因为
,因为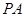 是圆
是圆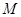 的切线
的切线所以经过
 三点的圆是以
三点的圆是以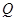 为圆心,以
为圆心,以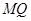 为半径的圆,
为半径的圆,故其方程为:
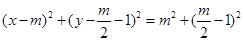 ........6分
........6分化简得:
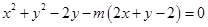 ,此式是关于
,此式是关于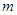 的恒等式,
的恒等式,故
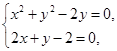 解得
解得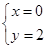 或
或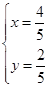
所以经过
 三点的圆必过定点
三点的圆必过定点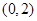 或
或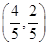 . ........10分
. ........10分(3)设
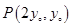 ,且
,且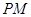 与
与 交于点
交于点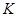 ,则
,则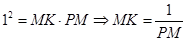
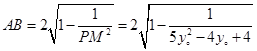 当
当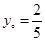 时,
时, 最小值为
最小值为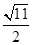 ...16分
...16分(几何方法酌情给分)

练习册系列答案
相关题目
 交圆
交圆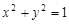 于A、B两点,且
于A、B两点,且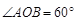 (O为原点),则实数
(O为原点),则实数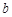 的值为 .
的值为 . :y="k" (x+2
:y="k" (x+2 )与圆O:
)与圆O: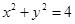 相交于A、B两点,O是坐标原点,
相交于A、B两点,O是坐标原点, ABO的面积为S.
ABO的面积为S.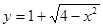 与直线
与直线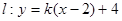 有两个交点时,实数
有两个交点时,实数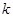 的取值范围是( )
的取值范围是( )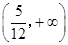

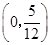
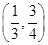
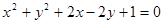 关于直线
关于直线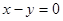 对称的圆的方程为 .
对称的圆的方程为 .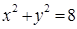 内有一点
内有一点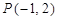 ,
, 为过点
为过点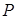 且倾斜角为
且倾斜角为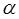 的弦,
的弦,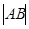 ;
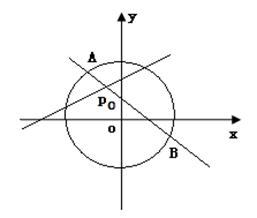
;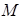 ,求点
,求点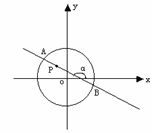
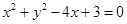 的圆心到直线
的圆心到直线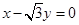 的距离是_____.
的距离是_____.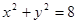 内有一点P0(-1,2),AB为过点P0且倾斜角为a的弦。
内有一点P0(-1,2),AB为过点P0且倾斜角为a的弦。