题目内容
求函数y=
思路解析:本题是一个复合函数,而且还有未知参数,因此首先要分类讨论,但是在分类讨论之前还要对指数部分的二次函数进行分析判断,在二次函数的单调区间中分类讨论未知参数以确定函数的单调区间和值域.
解:y=![]() =
=![]() .
.
令t=g(x)=-(x-1)2+3,t在区间(-∞,1]上递增,在区间[1,+∞)上递减.y=f(t)=at=f[g(x)].
当a>1时,y=f(t)=at递增,
∴y=f[g(x)]在区间(-∞,1]上递增,在区间[1,+∞)上递减.当x=1时ymax=a3,又y=at>0,∴函数的值域为(0,a3].
当0<a<1时,y=f(t)=at递减,
∴y=f[g(x)]在区间(-∞,1]上递减,在区间[1,+∞)上递增,当x=1时ymin=a3,函数的值域为[a3,+∞).

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 (a>0,且a≠1)的单调区间和值域.
(a>0,且a≠1)的单调区间和值域. 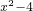 的单调区间.
的单调区间.