题目内容
已知f(x)=-log
(x2-ax+3a)在区间[2,+∞)上为增函数,则实数a的取值范围为
| 1 | 2 |
(-4,4]
(-4,4]
.分析:对数函数的真数必须是正数,这是解决对数问题优先考虑的;由于以
为底的对数函数是减函数,故对数函数的真数部分的二次函数要是增函数才行.
| 1 |
| 2 |
解答:解:∵f(x)=log _
(x2-ax+3a)在[2,+∞)上是减函数,
∴u=x2-ax+3a在[2,+∞)上为增函数,且在[2,+∞)上恒大于0.
∴得到:
解得:-4<a≤4,
则实数a的取值范围为(-4,4]
故答案为:(-4,4].
| 1 |
| 2 |
∴u=x2-ax+3a在[2,+∞)上为增函数,且在[2,+∞)上恒大于0.
∴得到:
|
解得:-4<a≤4,
则实数a的取值范围为(-4,4]
故答案为:(-4,4].
点评:处理函数问题的一个原则是定义域优先考虑,否则容易出错,另外复合函数的单调性问题,必须分开考虑.

练习册系列答案
相关题目
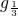 [3-(x-1)2],求f(x)的值域及单调区间.
[3-(x-1)2],求f(x)的值域及单调区间. [3-(x-1)2],求f(x)的值域及单调区间.
[3-(x-1)2],求f(x)的值域及单调区间.