题目内容
已知P为椭圆
上一点，F为右焦点，若
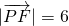，且点M满足
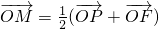（其中O为坐标原点），则
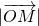的值为
- A.1
- B.2
- C.4
- D.8
B
分析：设椭圆的左焦点为F'，可得△PFF'中，OF'是中位线，有OM=
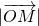PF'．再用椭圆的定义，得到PF'=2a-PF=4，所以OM=PF'=2，即的值为2．
解答：设椭圆的左焦点为F'，
∵点M满足，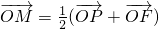
∴M是线段PF的中点，
又∵△PFF'中，O是FF'的中点
∴OM∥PF'且OM=PF'，
∵椭圆的长轴2a=10
∴根据椭圆的定义得：PF+PF'=10，可得PF'=10-PF=4
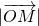因此，可得OM=PF'=2，即的值为2
故选B
点评：本题利用向量的形式，给出椭圆的焦点三角形PFF'中，OM是中位线，并求其长度，着重考查了向量的基本运算和椭圆的定义等知识点，属于中档题．
分析：设椭圆
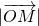的左焦点为F'，可得△PFF'中，OF'是中位线，有OM=PF'．再用椭圆的定义，得到PF'=2a-PF=4，所以OM=PF'=2，即的值为2．解答：设椭圆
的左焦点为F'，∵点M满足
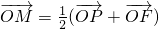，∴M是线段PF的中点，
又∵△PFF'中，O是FF'的中点
∴OM∥PF'且OM=
PF'，∵椭圆
的长轴2a=10∴根据椭圆的定义得：PF+PF'=10，可得PF'=10-PF=4
因此，可得OM=
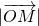PF'=2，即的值为2故选B
点评：本题利用向量的形式，给出椭圆的焦点三角形PFF'中，OM是中位线，并求其长度，着重考查了向量的基本运算和椭圆的定义等知识点，属于中档题．
练习册系列答案
相关题目
上一点，F1,F2是椭圆的焦点，∠F1PF2=900,则△F1PF2的面积为___________;
上一点,F1、F2是椭圆的两个焦点,
,则△F1PF2的面积是
.
，
，离心率为e，已知
，e，
成等比数列；
最大值．