题目内容

△ABC中，BC=2，角B=
π
3
，当△ABC的面积等于
3
2
时，sinC=（　　）
A．
3
2
B．
1
2
C．
3
3
D．
3
4
三角形面积为：
1
2
sinB•BC•BA=
1
2
×
3
2
×2×AB=
3
2

∴AB=1
由余弦定理可知：AC=
AB2+BC2-2AB•BC•cosB
=
3

∴由正弦定理可知
AB
sinC
=
AC
sinB

∴sinC=
sinB
AC
•AB=
1
2

故选B
练习册系列答案
相关题目
精英家教网在△ABC中，BC=2，AB+AC=3，中线AD的长为y，AB的长为x，建立y与x的函数关系式，并指出其定义域．
若△ABC中，BC=2，角B=
π
3
，当△ABC的面积等于
3
2
时，sinC为
1
2
1
2
．
（2013•石景山区二模）在△ABC中，BC=2，AC=
7
，B=
π
3
，则AB=
3
3
；△ABC的面积是
3
3
2
3
3
2
．
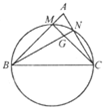如图，已知在△ABC中，BC=2，以BC为直径的圆分别交AB，AC于点M，N，MC与NB交于点G，若
BM
•
BC
=2，
CN
•
BC
=1，则∠BGC的度数为（　　）
在△ABC中，BC=2，AC=
7
，B=
π
3
，则△ABC的面积为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网