题目内容
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC= ,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( )
,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( )
A.

B.

C.

D.

【答案】分析:根据题意得ED∥BF,进而得到直线DE与平面BB1C1C所成的角等于直线BF与平面BB1C1C所成的角.利用几何体的结构特征得到∠FBG=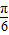 .即可得到答案.
.即可得到答案.
解答:解:取AC的中点为F,连接BF、DF.
因为在直三棱柱ABC-A1B1C1中,且D,E分别是AC1和BB1的中点,
所以ED∥BF.
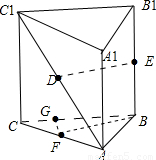
过点F作FG垂直与BC交BC 与点G,由题意得∠FBG即为所求的角.
因为AB=1,AC=2,BC=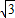 ,所以∠ABC=
,所以∠ABC=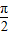 ,∠BCA=
,∠BCA=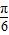 °,
°,
所以在△FBG中∠FBG=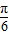 .
.
故选A.
点评:解决此类问题的关键是熟悉线面角的作法,即由线上的一点作平面的垂线再连接斜足与垂足则得到线面角.
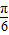 .即可得到答案.
.即可得到答案.解答:解:取AC的中点为F,连接BF、DF.
因为在直三棱柱ABC-A1B1C1中,且D,E分别是AC1和BB1的中点,
所以ED∥BF.

过点F作FG垂直与BC交BC 与点G,由题意得∠FBG即为所求的角.
因为AB=1,AC=2,BC=
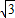 ,所以∠ABC=
,所以∠ABC=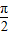 ,∠BCA=
,∠BCA=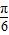 °,
°,所以在△FBG中∠FBG=
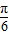 .
.故选A.
点评:解决此类问题的关键是熟悉线面角的作法,即由线上的一点作平面的垂线再连接斜足与垂足则得到线面角.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目




