题目内容
在△ABC中，∠ACB=90°，AB=16，∠ABC=30°，SC⊥平面ABC，SC=8，M是AB边上一动点，则SM的最小值为 ．
分析：S是定点，要使SM的值最小，只需使SM⊥AB即可．要使SM⊥AB，由于SC⊥平面ABC，只需使CM⊥AB即可．所以作CM⊥AB，连接SM，此时的SM最短，在三角形ABC中，根据AB和sin∠ABC利用三角函数求出CM的长，然后在直角三角形SCM中，由SC和CM根据勾股定理即可求出PM的长．
解答：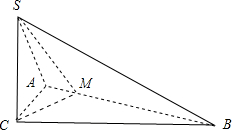
解：过C作CM⊥AB，连接SM，因为SC⊥AB，所以AB⊥平面SCM，
所以SM⊥AB，此时SM最短，
∵∠ABC=30°，AB=16，
∴AC=AB•sin30°=8．
∴CM=AC•cos30°=8•
=4
．
∴SM=
=
=4
故答案为：4
解：过C作CM⊥AB，连接SM，因为SC⊥AB，所以AB⊥平面SCM，所以SM⊥AB，此时SM最短，
∵∠ABC=30°，AB=16，
∴AC=AB•sin30°=8．
∴CM=AC•cos30°=8•
| ||
| 2 |
| 3 |
∴SM=
| PC2+CM2 |
| 64+48 |
| 7 |
故答案为：4
| 7 |
点评：此题是一道综合题，要求学生掌握直线与平面垂直的条件与性质，会根据条件解直角三角形，灵活运用勾股定理求边长．解此题的关键是利用直线与平面垂直的性质和判定作出辅助线确定出最短的线段．
练习册系列答案
相关题目
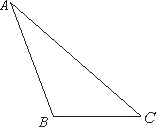如图，在△ABC中，AC=2，BC=1，
如图，在△ABC中，AC=BC，AB=2，O为AB的中点，沿OC将△AOC折起到△A′OC的位置，使得直线A′B与平面ABC成30°角．