题目内容
(本小题9分)
如图,四棱锥S—ABCD的底面是正方形,SD 平面ABCD,SD=2a,
平面ABCD,SD=2a, ,点E是SD上的点,且
,点E是SD上的点,且

(Ⅰ)求证:对任意的 ,都有
,都有
(Ⅱ)设二面角C—AE—D的大小为
 ,直线BE与平面ABCD所成的角为
,直线BE与平面ABCD所成的角为 ,若
,若 ,求
,求 的值
的值
(Ⅰ)见解析;
(Ⅱ)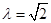
【解析】(1)可以通过证明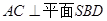 即可。
即可。
(II)先找出二面角C-AE-D的平面角∠CDF,即∠CDF=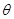 .直线BE与平面ABCD所成的角
.直线BE与平面ABCD所成的角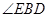 ,即
,即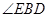 =
=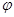 .然后再根据
.然后再根据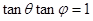 建立关于
建立关于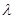 的方程,解出
的方程,解出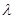 的值。
的值。
解:Ⅰ)证法1:如图1,连接BE、BD,
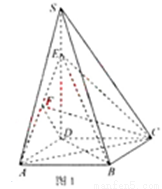
由底面ABCD是正方形可得AC⊥BD。
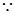 SD⊥平面ABCD,
SD⊥平面ABCD,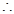 BD是BE在平面ABCD上的射影,
BD是BE在平面ABCD上的射影,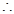 AC⊥BE
------3分
AC⊥BE
------3分
(Ⅱ)如图1,

由SD⊥平面ABCD知,∠DBE= 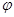 ,
,
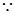 SD⊥平面ABCD,CD
SD⊥平面ABCD,CD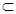 平面ABCD,
平面ABCD,  SD⊥CD。
SD⊥CD。
又底面ABCD是正方形, CD⊥AD,而SD
CD⊥AD,而SD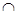 AD=D,CD⊥平面SAD.
AD=D,CD⊥平面SAD.
连接AE、CE,过点D在平面SAD内作DE⊥AE于F,连接CF,则CF⊥AE,
故∠CDF是二面角C-AE-D的平面角,即∠CDF=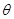 。
------------------5分
。
------------------5分
在Rt△BDE中,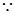 BD=2a,DE=
BD=2a,DE=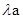
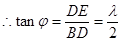
在Rt△ADE中, 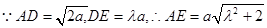
从而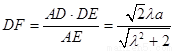 在
在 中,
中,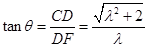 --7分
--7分
由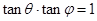 ,得
,得
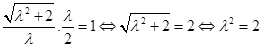 .
.
由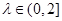 ,解得
,解得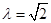 ,即为所求.
---------------------------------9分
,即为所求.
---------------------------------9分
(1)证法2:以D为原点,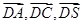 的方向分别作为x,y,z轴的正方向建立如
的方向分别作为x,y,z轴的正方向建立如
图2所示的空间直角坐标系,
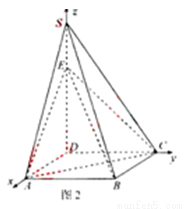
则:D(0,0,0),A(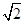 ,0,0),B(
,0,0),B(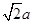 ,
,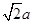 ,0),C(0,
,0),C(0,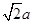 ,0),E(0,0
,0),E(0,0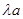 ),---------2分
),---------2分
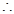

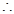
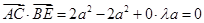 , 即
, 即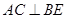 。
---------3分
。
---------3分
解法2:
由(I)得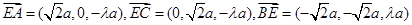 .
.
设平面ACE的法向量为n=(x,y,z),则由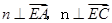 得
得
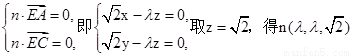 。--------------------5分
。--------------------5分
易知平面ABCD与平面ADE的一个法向量分别为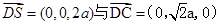 .
. 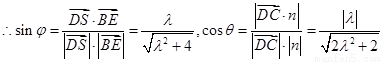 -------------7分
-------------7分
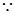 0<
0<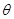 ,
,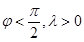 ,
,
 =1
=1

由于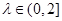 ,解得
,解得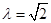 ,即为所求。--------------------9分
,即为所求。--------------------9分

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
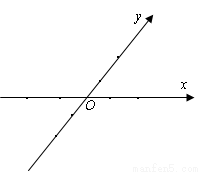
 中,
中,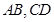 为底面圆的两条直径,
为底面圆的两条直径, ,且
,且 ⊥
⊥ ,
, ,
,
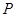 为
为 的中点.
的中点. ∥平面
∥平面 ;
; 所成角的正切值.
所成角的正切值. 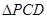 沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。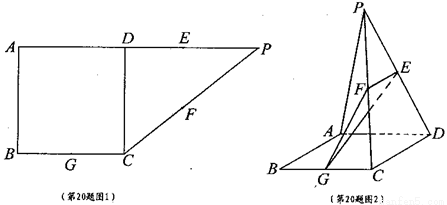
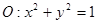 和定点
和定点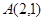 ,由圆
,由圆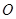 外一点
外一点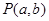 向圆
向圆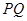 ,切点为
,切点为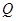 ,且满足
,且满足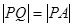
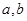 间满足的等量关系;(2)求线段
间满足的等量关系;(2)求线段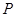 为圆心所作的圆
为圆心所作的圆