题目内容
设点M(a,b)是曲线C:y=
x2+lnx+2上的任意一点,直线l是曲线C在点M处的切线,那么直线l斜率的最小值为( )
| 1 |
| 2 |
| A、-2 | B、0 | C、2 | D、4 |
分析:先求出函数的定义域,然后求出在x=a处的导数,最后利用均值不等式求出最值即可,注意等号成立的条件.
解答:解:曲线C:y=
x2+lnx+2定义域为(0,+∞)
y'=x+
则y'|x=a=a+
≥2当且仅当a=1时直线l斜率的最小值
故选C
| 1 |
| 2 |
y'=x+
| 1 |
| x |
| 1 |
| a |
故选C
点评:考查学生会利用导数求曲线上过某点切线方程的斜率,以及利用均值不等式求最值,掌握不等式成立时的条件,属于基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 上的任意一点,直线l是曲线C在点M处的切线,那么直线l斜率的最小值为( )
上的任意一点,直线l是曲线C在点M处的切线,那么直线l斜率的最小值为( )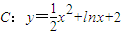 上的任意一点,直线l是曲线C在点M处的切线,那么直线l斜率的最小值为( )
上的任意一点,直线l是曲线C在点M处的切线,那么直线l斜率的最小值为( )