题目内容
 如图所示,若D是△ABC内的一点,且AB2-AC2=DB2-DC2.求证:AD⊥BC.
如图所示,若D是△ABC内的一点,且AB2-AC2=DB2-DC2.求证:AD⊥BC.分析:设
=
,
=
,
=
,
=
,
=
,将
=
+
、
=
+
代入
2-
2的式子,化简整理
2-
2=
2+2
•
-2
•
-
2,结合题意
2-
2=
2-
2化简,可得
•(
-
)=0,再结合向量的加减法法则得到
•
=0,由此结合数量积的性质即可得到AD⊥BC.
| AB |
| a |
| AC |
| b |
| AD |
| e |
| DB |
| c |
| DC |
| d |
| a |
| e |
| c |
| b |
| e |
| d |
| a |
| b |
| a |
| b |
| c |
| e |
| c |
| e |
| d |
| d |
| a |
| b |
| c |
| d |
| e |
| c |
| d |
| AD |
| BC |
解答:解:设
=
,
=
,
=
,
=
,
=
,
则
=
+
,
=
+
.
∴
2-
2=(
+
)2-(
+
)2
=
2+2
•
-2
•
-
2.
∵由已知AB2-AC2=DB2-DC2,得
2-
2=
2-
2,
∴
2+2
•
-2
•
-
2=
2-
2,即
•(
-
)=0.
∵
=
+
=
-
,∴
•
=
•(
-
)=0,
因此,可得
⊥
,即AD⊥BC.
| AB |
| a |
| AC |
| b |
| AD |
| e |
| DB |
| c |
| DC |
| d |
则
| a |
| e |
| c |
| b |
| e |
| d |

∴
| a |
| b |
| e |
| c |
| e |
| d |
=
| c |
| e |
| c |
| e |
| d |
| d |
∵由已知AB2-AC2=DB2-DC2,得
| a |
| b |
| c |
| d |
∴
| c |
| e |
| c |
| e |
| d |
| d |
| c |
| d |
| e |
| c |
| d |
∵
| BC |
| BD |
| DC |
| d |
| c |
| AD |
| BC |
| e |
| d |
| c |
因此,可得
| AD |
| BC |
点评:本题给出三角形ABC内满足平方关系的点D,求证AD⊥BC.着重考查了平面向量的加减法则、向量的数量积及其运算性质等知识,属于中档题.

练习册系列答案
相关题目
 已知函数f(x)的定义域为[-2,+∞),部分对应值如下表,
已知函数f(x)的定义域为[-2,+∞),部分对应值如下表,| x | -2 | 0 | 4 |
| f(x) | 1 | -1 | 1 |
| b+3 |
| a+3 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(-
|
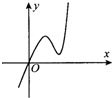 定义在R上的函数f(x)满足f(4)=1.f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示.若两正数a,b满足f(2a+b)<1,则
定义在R上的函数f(x)满足f(4)=1.f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示.若两正数a,b满足f(2a+b)<1,则| b+2 |
| a+2 |
A、(
| ||||
B、(-∞,
| ||||
C、(
| ||||
| D、(-∞,-3) |
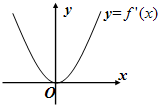 已知f(x)是定义域为R的奇函数,f(-4)=-1,f(x)的导函数f′(x)的图象如图所示.若两正数a,b满足f(a+2b)<1,则
已知f(x)是定义域为R的奇函数,f(-4)=-1,f(x)的导函数f′(x)的图象如图所示.若两正数a,b满足f(a+2b)<1,则| a+2 |
| b+2 |
A、(
| ||
B、(
| ||
| C、(-1,10) | ||
| D、(-∞,-1) |
 已知函数f(x)的定义域为[-2,+∞),部分对应值如下表,
已知函数f(x)的定义域为[-2,+∞),部分对应值如下表,| x | -2 | 0 | 4 |
| f(x) | 1 | -1 | 1 |
| b+3 |
| a+3 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
 已知f(x)是定义域为R的奇函数,f(-4)=-2,f(x)的导函数f′(x)的图象如图所示,若两正数a,b满足f(a+2b)<2,则
已知f(x)是定义域为R的奇函数,f(-4)=-2,f(x)的导函数f′(x)的图象如图所示,若两正数a,b满足f(a+2b)<2,则