题目内容
已知点 是抛物线
是抛物线 的焦点,
的焦点, 是抛物线上的两点,
是抛物线上的两点, ,则线段
,则线段 的中点到
的中点到 轴的距离为( )
轴的距离为( )
A. B.
B. C.
C. D.
D.
【答案】
C
【解析】
试题分析:根据抛物线的方程求出准线方程,利用抛物线的定义抛物线上的点到焦点的距离等于到准线的距离,列出方程求出A,B的中点横坐标,求出线段AB的中点到y轴的距离。根据题意,由于点 是抛物线
是抛物线 的焦点,则为F(
的焦点,则为F( ),准线方程为
),准线方程为 ,则根据设
,则根据设

故可知线段 的中点到
的中点到 轴的距离为
轴的距离为 ,选C.
,选C.
考点:抛物线的定义
点评:本题考查解决抛物线上的点到焦点的距离问题,利用抛物线的定义将到焦点的距离转化为到准线的距离

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 是抛物线
是抛物线 :
: 的焦点,则
的焦点,则 _______.
_______.
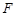 为抛物线
为抛物线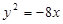 的焦点,
的焦点,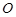 为原点,点
为原点,点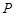 是抛物线准线上一动点,点
是抛物线准线上一动点,点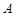 在抛物线上,且
在抛物线上,且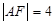 ,则
,则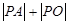 的最小值为 ( )
的最小值为 ( )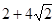 C.
C.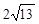 D.
D.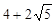
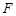 为抛物线
为抛物线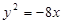 的焦点,
的焦点,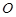 为原点,点
为原点,点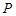 是抛物线准线上一动点,点
是抛物线准线上一动点,点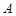 在抛物线上,且
在抛物线上,且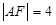 ,则
,则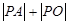 的最小值为 ( )
的最小值为 ( ) C.
C.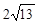 D.
D.
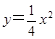 的焦点,P是该抛物线上的动点,则线段PF中点的轨迹方程是( )
的焦点,P是该抛物线上的动点,则线段PF中点的轨迹方程是( )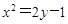 B.
B. C.
C.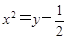 D.
D.