题目内容
通过市场调查,得到某产品的资金投入x(万元)与获得的利润y(万元)的数据,如下表所示:,
XiYi=117
(1)根据上表提供的数据,用最小二乘法求线性回归直线方程
=bx+a;
(2)现投入资金10(万元),求估计获得的利润为多少万元.
| 资金入x | 2 | 3 | 4 | 5 | 6 |
| 利润 y | 2 | 3 | 5 | 6 | 9 |
| 5 |
 |
| i=1 |
(1)根据上表提供的数据,用最小二乘法求线性回归直线方程
 |
| y |
(2)现投入资金10(万元),求估计获得的利润为多少万元.
分析:(1)根据所给的数据,做出横标和纵标的平均数,利用最小二乘法求出线性回归方程的系数,代入样本中心点求出a的值,写出线性回归方程.
(2)根据上一问做出的线性回归方程,代入所给的x的数据,预报出获得利润的值.
(2)根据上一问做出的线性回归方程,代入所给的x的数据,预报出获得利润的值.
解答:解:(1)根据所给的数据得到
=
=4
=
=5
∴
=
=1.7
a=5-1.9×4=-1.8
∴线性回归方程是y=1.7x-1.8
(2)根据上一问做出的线性回归方程,
把x=10(万元)代入线性回归方程得到y=1.7×10-1.8=15.2(万元)
答:(1)线性回归方程是y=1.7x-1.8
(2)当x=10时,预报y的值是15.2万元
. |
| x |
| 2+3+4+5+6 |
| 5 |
. |
| y |
| 2+3+5+6+9 |
| 5 |
∴
 |
| b |
| 2×2+3×3+4×5+5×6+6×9-5×4×5 |
| 4+9+16+25+36-5×16 |
a=5-1.9×4=-1.8
∴线性回归方程是y=1.7x-1.8
(2)根据上一问做出的线性回归方程,
把x=10(万元)代入线性回归方程得到y=1.7×10-1.8=15.2(万元)
答:(1)线性回归方程是y=1.7x-1.8
(2)当x=10时,预报y的值是15.2万元
点评:本题考查线性回归方程是求法和应用,本题解题的关键是正确运算线性回归方程的系数,要说明得到的结果是一个预报值,本题是一个中档题目.

练习册系列答案
相关题目
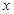 (万元)与获得的利润
(万元)与获得的利润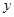 (万元)的数据,如下表所示:
(万元)的数据,如下表所示: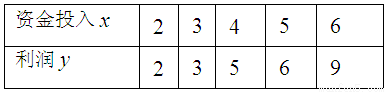
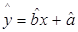 ;
;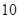 (万元),求估计获得的利润为多少万元.
(万元),求估计获得的利润为多少万元.