题目内容
袋中有4个红球,3个黑球,从袋中随机地抽取4个球,设取到一个红球得2分,取到一个黑球得1分.(1)求得分X不大于6的概率;
(2)求得分X的数学期望.
【答案】分析:(1)取到一个红球得2分,取到一个黑球得1分,所以得分x=5,6,8,因为从袋中随机地抽取4个球,总共有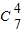 种取法,然后根据概率公式进行求解;
种取法,然后根据概率公式进行求解;
(2)根据题意求得分X的数学期望,x可以取5,6,7,8,分别求出相对应的概率,然后列出分布列,然后利用数学期望公式进行求解;
解答:解:(1)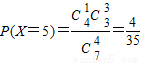 ,
,
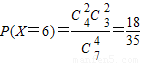 ,
,
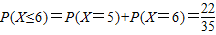 (4分)
(4分)
(2)得分X的所有可能值为:5,6,7,8,
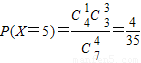 ,
,
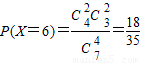 ,
,
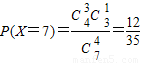 ,
,
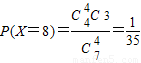 ,
,
得分X的分布列为
EX=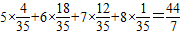 .(10分)
.(10分)
点评:此题主要考查离散型随机变量的期望与公式,这是高考必考的热点问题,比较简单,是一到中档题;
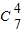 种取法,然后根据概率公式进行求解;
种取法,然后根据概率公式进行求解;(2)根据题意求得分X的数学期望,x可以取5,6,7,8,分别求出相对应的概率,然后列出分布列,然后利用数学期望公式进行求解;
解答:解:(1)
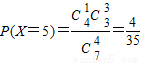 ,
,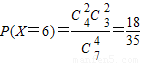 ,
,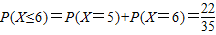 (4分)
(4分)(2)得分X的所有可能值为:5,6,7,8,
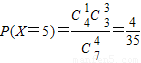 ,
,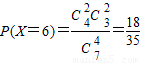 ,
,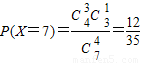 ,
,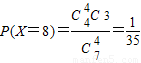 ,
,得分X的分布列为
| X | 5 | 6 | 7 | 8 |
| P | 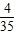 | 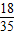 | 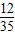 | 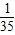 |
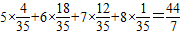 .(10分)
.(10分)点评:此题主要考查离散型随机变量的期望与公式,这是高考必考的热点问题,比较简单,是一到中档题;

练习册系列答案
相关题目