题目内容
椭圆 的两个焦点为
的两个焦点为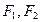 ,点
,点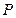 在椭圆
在椭圆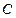 上,
上,
且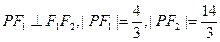 ,
,
(1)求椭圆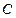 的方程;
的方程;
(2)试确定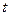 的取值范围,使得椭圆上有两个不同的点关于直线
的取值范围,使得椭圆上有两个不同的点关于直线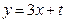 对称.
对称.
 的两个焦点为
的两个焦点为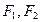 ,点
,点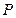 在椭圆
在椭圆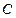 上,
上,且
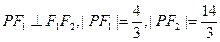 ,
,(1)求椭圆
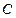 的方程;
的方程;(2)试确定
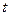 的取值范围,使得椭圆上有两个不同的点关于直线
的取值范围,使得椭圆上有两个不同的点关于直线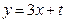 对称.
对称.(1)椭圆方程为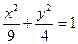 ;(2)-
;(2)-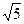 <t<
<t<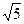 .
.
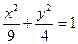 ;(2)-
;(2)-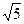 <t<
<t<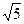 .
. (1)因为点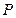 在椭圆上,
在椭圆上,
∴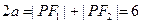 ,
,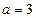
在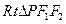 中,
中,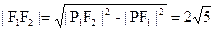
∴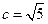 ,
,
∴ ,
,
∴椭圆方程为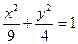 ;
;
(2)设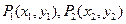 为椭圆上关于直线
为椭圆上关于直线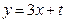 对称的两点,
对称的两点,
则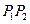 所在的直线方程是
所在的直线方程是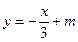 ,
,
联立方程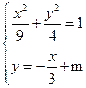 ,
,
整理得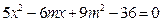 ,
,
 ,
,
∴ ,
,
又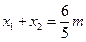 , 可得
, 可得 ,
,
∴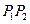 的中点坐标为
的中点坐标为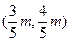 ,且该点在直线
,且该点在直线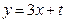 上
上
∴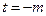 , ∴ -
, ∴ -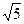 <t<
<t<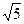 .
.
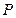 在椭圆上,
在椭圆上,∴
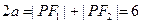 ,
,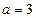
在
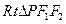 中,
中,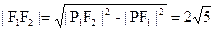
∴
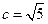 ,
,∴
 ,
,∴椭圆方程为
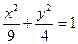 ;
;(2)设
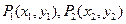 为椭圆上关于直线
为椭圆上关于直线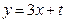 对称的两点,
对称的两点,则
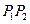 所在的直线方程是
所在的直线方程是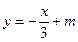 ,
, 联立方程
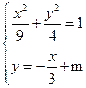 ,
,整理得
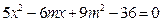 ,
, ,
, ∴
 ,
,又
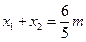 , 可得
, 可得 ,
, ∴
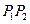 的中点坐标为
的中点坐标为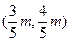 ,且该点在直线
,且该点在直线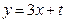 上
上∴
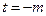 , ∴ -
, ∴ -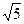 <t<
<t<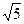 .
. 
练习册系列答案
相关题目




 为椭圆上任意一点,以
为椭圆上任意一点,以 为半径作圆
为半径作圆 有公共点时,求△
有公共点时,求△ 面积的最大值
面积的最大值 中,已知
中,已知 ,且当顶点
,且当顶点 位于定点
位于定点 时,
时, 有最小值为
有最小值为 .(1)建立适当的坐标系,求顶点
.(1)建立适当的坐标系,求顶点 作直线与(1)中的曲线交于
作直线与(1)中的曲线交于 、
、 两点,求
两点,求 的最小值的集合.
的最小值的集合. ,1)、P2(-
,1)、P2(- ,-
,- ),求椭圆的方程.
),求椭圆的方程.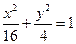 ,过点
,过点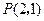 引1条弦,使它在这点平分,求此弦所在直线方程.
引1条弦,使它在这点平分,求此弦所在直线方程. =1表示焦点在y轴上的椭圆,则m的取值范围是( )
=1表示焦点在y轴上的椭圆,则m的取值范围是( ) 。
。 ,
, ,则
,则 的轨迹方程是
的轨迹方程是