题目内容
设f(x)是R上的奇函数,当x>0时,f(x)=2x+2012x,则当x<0时,f(x)=( )A.
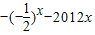
B.
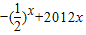
C.-2x-2012
D.-2x+2012
【答案】分析:当x<0时,-x>0,由已知表达式可求出f(-x),再由奇函数的性质可求f(x).
解答:解:当x<0时,则-x>0,∴f(-x)=2-x-2012x,
又∵f(x)为奇函数,
∴f(x)=-f(-x)=-(2-x-2012x)=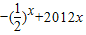 .
.
故选B.
点评:本题考查函数解析式的求法及函数的奇偶性,属基础题,难度不大.
解答:解:当x<0时,则-x>0,∴f(-x)=2-x-2012x,
又∵f(x)为奇函数,
∴f(x)=-f(-x)=-(2-x-2012x)=
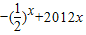 .
.故选B.
点评:本题考查函数解析式的求法及函数的奇偶性,属基础题,难度不大.

练习册系列答案
相关题目