题目内容
甲、乙两个学校高三年级分别有1100人,1000人,为了统计两个学校在本地区一模考试的数学科目的成绩,采用分层抽样抽取了105名学生的成绩,并作了如下频率分布表.(规定成绩在[130,150]内为优秀)
甲校:
乙校:
(I)计算x,y的值,并分别估计两个学校在此次一模考试中数学成绩的优秀率(精确到0.0001);
(II)由以上统计数据填写下面的2×2列联表,并判断是否有90%的把握认为两个学校的数学成绩有差异,并说明理由.
附:K2=
甲校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
(II)由以上统计数据填写下面的2×2列联表,并判断是否有90%的把握认为两个学校的数学成绩有差异,并说明理由.
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥K0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
分析:(1)根据要抽取的人数和两个学校的人数利用分层抽样得到两个学校要抽取的人数,分别做出x,y的值,利用平均数的公式做出两个学校的平均分.
(2)根据数学成绩不低于130分为优秀,低于130分为非优秀,看出优秀的人数和不优秀的人数,填出列联表,根据列联表的数据,写出观测值的计算公式,得到观测值,同临界值进行比较,得到在犯错误的概率不超过0.1的前提下认为“两个学校的数学成绩有差异”.
(2)根据数学成绩不低于130分为优秀,低于130分为非优秀,看出优秀的人数和不优秀的人数,填出列联表,根据列联表的数据,写出观测值的计算公式,得到观测值,同临界值进行比较,得到在犯错误的概率不超过0.1的前提下认为“两个学校的数学成绩有差异”.
解答:解:(1)依题甲校抽取55人,乙校抽取50,
故x=6,y=7
估计甲校优秀率为
≈0.0727,
乙校优秀率为
=0.2000.
(2)根据所给的条件列出列联表
k2=
≈3.671,
又因为3.671>2.706,
故有90%的把握认为两个学校的数学成绩有差异.
故x=6,y=7
估计甲校优秀率为
| 4 |
| 55 |
乙校优秀率为
| 10 |
| 50 |
(2)根据所给的条件列出列联表
| 甲校 | 乙校 | 总计 | |
| 优秀 | 4 | 10 | 14 |
| 非优秀 | 51 | 40 | 91 |
| 总计 | 55 | 50 | 105 |
| 105×(4×40-10×51)2 |
| 55×50×14×91 |
又因为3.671>2.706,
故有90%的把握认为两个学校的数学成绩有差异.
点评:本题主要考查独立性检验的应用,解题的关键是正确运算出观测值,理解临界值对应的概率的意义,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
甲乙两个学校高三年级分别为1100人,1000人,为了统计两个学校在地区二模考试的数学科目成绩,采用分层抽样抽取了105名学生的成绩,并作出了部分频率分布表如下:(规定考试成绩在[120,150]内为优秀)
甲校:
乙校:
(1)计算x,y的值,并分别估计两上学校数学成绩的优秀率;
(2)由以上统计数据填写下面2×2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
附:k2=
甲校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
(2)由以上统计数据填写下面2×2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(k2≥k0) | 0.10 | 0.025 | 0.010 |
| k0 | 2.706 | 5.024 | 6.635 |
甲、乙两个学校高三年级分别有1100人,1000人,为了统计两个学校在本地区一模考试的数学科目的成绩,采用分层抽样抽取了105名学生的成绩,并作了如下频率分布表.(规定成绩在[130,150]内为优秀)
甲校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
(II)由以上统计数据填写下面的2×2列联表,并判断是否有90%的把握认为两个学校的数学成绩有差异,并说明理由.
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
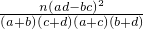
| P(K2≥K0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
(本小题满分12分)
甲、乙两个学校高三年级分别有1100人,1000人,为了统计两个学校在本地区一模考试的数学科目的成绩,采用分层抽样抽取了105名学生的成绩,并作了如下频率分布表。(规定成绩在![]() 内为优秀)
内为优秀)
甲校:
| 分组 |
|
|
|
|
|
|
|
|
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
乙校:
| 分组 |
|
|
|
|
|
|
|
|
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
(I)计算x,y的值,并分别估计两个学校在此次一模考试中数学成绩的优秀率(精确到0.0001);
(II)由以上统计数据填写下面的2×2列联表,并判断是否有90%的把握认为两个学校的数学成
绩有差异,并说明理由。
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
附:![]()
|
| 0.10 | 0.05 | 0.025 | 0.010 |
|
| 2.706 | 3.841 | 5.024 | 6.635 |