题目内容
利用导数求和
(1)Sn=1+2x+3x2+…+nxn-1(x≠0,n∈N*)
(2)Sn=C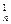 +2C
+2C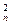 +3C
+3C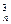 +…+nC
+…+nC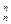 ,(n∈N*)
,(n∈N*)
(1)Sn=1+2x+3x2+…+nxn-1(x≠0,n∈N*)
(2)Sn=C
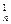 +2C
+2C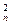 +3C
+3C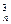 +…+nC
+…+nC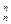 ,(n∈N*)
,(n∈N*)(1) Sn=1+2x+3x2+…+nxn-1=
(2)Sn=C +2C
+2C +…+nC
+…+nC =n·2n-1
=n·2n-1

(2)Sn=C
 +2C
+2C +…+nC
+…+nC =n·2n-1
=n·2n-1(1)当x=1时,Sn=1+2+3+…+n= n(n+1);
n(n+1);
当x≠1时,
∵x+x2+x3+…+xn= ,
,
两边都是关于x的函数,求导得
(x+x2+x3+…+xn)′=( )′
)′
即Sn=1+2x+3x2+…+nxn-1=
(2)∵(1+x)n=1+C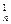 x+C
x+C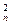 x2+…+C
x2+…+C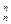 xn,
xn,
两边都是关于x的可导函数,求导得
n(1+x)n-1=C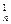 +2C
+2C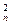 x+3C
x+3C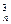 x2+…+nC
x2+…+nC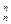 xn-1,
xn-1,
令x=1得,n·2n-1=C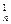 +2C
+2C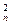 +3C
+3C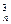 +…+nC
+…+nC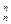 ,
,
即Sn=C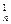 +2C
+2C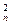 +…+nC
+…+nC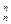 =n·2n-1。
=n·2n-1。
 n(n+1);
n(n+1);当x≠1时,
∵x+x2+x3+…+xn=
 ,
,两边都是关于x的函数,求导得
(x+x2+x3+…+xn)′=(
 )′
)′即Sn=1+2x+3x2+…+nxn-1=

(2)∵(1+x)n=1+C
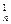 x+C
x+C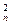 x2+…+C
x2+…+C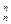 xn,
xn,两边都是关于x的可导函数,求导得
n(1+x)n-1=C
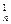 +2C
+2C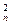 x+3C
x+3C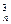 x2+…+nC
x2+…+nC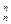 xn-1,
xn-1,令x=1得,n·2n-1=C
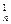 +2C
+2C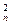 +3C
+3C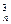 +…+nC
+…+nC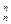 ,
,即Sn=C
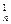 +2C
+2C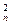 +…+nC
+…+nC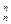 =n·2n-1。
=n·2n-1。
练习册系列答案
相关题目
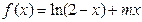 在区间
在区间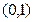 上是增函数.(1)求实数m的取值范围;(2)若数列
上是增函数.(1)求实数m的取值范围;(2)若数列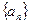 满足
满足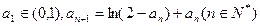 ,证明:
,证明: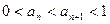 .
.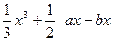 (a,b∈R),在其图象上一点P(x,y)处的切线的斜率记为f(x).
(a,b∈R),在其图象上一点P(x,y)处的切线的斜率记为f(x).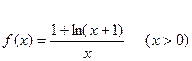 ,
,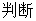
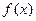 在区间
在区间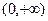 是增函数还是减函数?并证明你的结论;
是增函数还是减函数?并证明你的结论;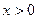 时,
时,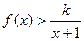 恒成立,求整数
恒成立,求整数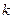 的最小值。
的最小值。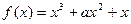 ,
,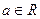 是常数,
是常数,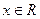 .
.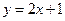 是曲线
是曲线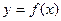 的一条切线,求
的一条切线,求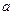 的值;
的值;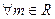 ,试证明
,试证明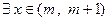 ,使
,使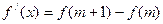 .
.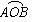 上求一点P,当△PAB面积最大时,P点坐标为 .
上求一点P,当△PAB面积最大时,P点坐标为 .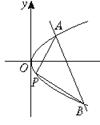
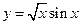 导数为( )
导数为( )


