题目内容

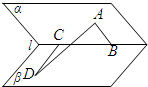
如图，二面角α-l-β的棱l上有两点B、C，AB⊥l，CD⊥l，且AB⊆α，CD⊆β，若AB=CD=BC=2，AD=4，则此二面角的大小为______．
由条件，知
BC
•
AB
=0，
BC
•
CD
=0，
AD
=
AB
+
BC
+
CD

所以
AD
2=
AB
2+
BC
2+
CD
2+2
AB
•
BC
+2
BC
•
CD
+
AB
•
CD

=4+4+4+2×2×2cos＜
AB，
CD
＞=16
∴cos＜
AB，
CD
＞=
1
2

所以
＜AB，
CD
＞=60°，＜
BA，
CD
＞=120°
所以二面角的大小为120°
故答案为120°．
练习册系列答案
相关题目
如图几何体中，四边形ABCD为矩形，AB=3BC=6，EF =4，BF=CF=AE=DE=2，  EF∥AB，G为FC的中点，M为线段CD上的一点，且CM =2．
（1）证明：平面BGM⊥平面BFC；
（2）求三棱锥F－BMC的体积V．
平面α与平面β相交成一个锐二面角θ，平面α上的一个圆在平面β上的射影是一个离心率为
1
2
的椭圆，则θ等于（　　）
A．30°B．45°C．60°D．75°
如图，已知正三棱柱ABC=A1B1C1的各棱长都是4，E是BC的中点，动点F在侧棱CC1上，且不与点C重合．
（Ⅰ）当CF=1时，求证：EF⊥A1C；
（Ⅱ）设二面角C-AF-E的大小为θ，求tanθ的最小值．
已知三棱柱ABC-A1B1C1的底面为直角三角形，则棱与底面垂直，如图所示，D是棱CC1的中点，且∠ACB=90°，BC=1，AC=
3
，AA1=
6

（Ⅰ）证明：A1D⊥平面AB1C1；
（Ⅱ）求二面角B-AB1-C1的余弦值．
在直三棱柱ABC-A1B1C1中，AC=BC=2，AA1=2
2
，∠ACB=90°，M是AA1的中点，N是BC1的中点
（1）求证：MN∥平面A1B1C1；
（2）求点C1到平面BMC的距离；
（3）求二面角B-C1M-A1的平面角的余弦值大小．
已知二面角α-AB-β为120°，AC?α，BD?β，且AC⊥AB，BD⊥AB，AB=AC=BD=a，则CD的长为______．
如图，矩形ABCD和直角梯形BEFC所在平面互相垂直，∠BCF-90°，BE∥CF，CE⊥EF，AD=
3
，EF=2．
（1）求异面直线AD与EF所成的角；
（2）当AB的长为何值时，二面角A-EF-C的大小为45°？
在正方体ABCD－A1B1C1D1中，点M，N分别在线段AB1，BC1上，且AM＝BN.以下结论：①AA1⊥MN；②A1C1∥MN；③MN∥平面A1B1C1D1；④MN与A1C1异面，其中有可能成立的个数为(　　)
A．4 B．3C．2 D．1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网