题目内容
【题目】在数列{an}中,a1=1,a2=![]() ,an+1-
,an+1-![]() an+an-1=0 (n≥2,且n∈N*),若数列{an+1+λan}是等比数列.
an+an-1=0 (n≥2,且n∈N*),若数列{an+1+λan}是等比数列.
(1)求实数λ;
(2)求数列{an}的通项公式;
(3)设![]() ,求证:
,求证: ![]() .
.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)利用新数列为等比数列和递推公式,通过待定系数法进行求解;(2)利用(1)结论得到关于![]() 的方程组进行求解;(3)利用放缩法和等比数列的求和公式进行求解.
的方程组进行求解;(3)利用放缩法和等比数列的求和公式进行求解.
试题解析:(1)由数列{an+1+λan}是等比数列,可设an+1+λan=μ(an+λan-1) (n≥2).
∴an+1+(λ-μ)an-λμan-1=0,
∵an+1-![]() an+an-1=0,
an+an-1=0,
∴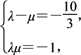 ∴λ=-
∴λ=-![]() 或λ=-3.
或λ=-3.
(2)解 由(1)知,n≥2,λ=-![]() 时,
时,
an-![]() an-1=3n-1,①
an-1=3n-1,①
n≥2,λ=-3时,an-3an-1=![]() .②
.②
由①②可得an=![]()
![]() (n≥2),当n=1时,也符合.
(n≥2),当n=1时,也符合.
∴an=![]() (3n-
(3n-![]() ),n∈N*.
),n∈N*.
(3)证明 由(2)知,
an=![]()
![]() >0,
>0,
∵an-3an-1=![]() ,∴an>3an-1,
,∴an>3an-1,
∴![]() <
<![]() ·
·![]() (n≥2).
(n≥2).
∴Sn<![]() +
+![]()
![]() =
=![]() +
+![]()
![]() -
-![]() <
<![]() +
+![]() Sn.
Sn.
∴Sn<![]() .
.

练习册系列答案
相关题目