题目内容
某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况，随机抽查了该市当天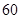
名网友的网购金额情况，得到如下数据统计表（如图）：
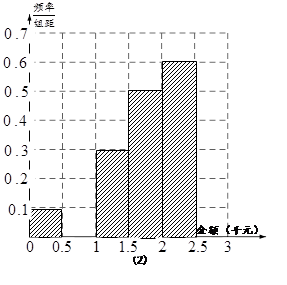
若网购金额超过
千元的顾客定义为“网购达人”，网购金额不超过千元的顾客定义为“非网购达人”，已知“非网购达人”与“网购达人”人数比恰好为
．
（1）试确定
，
，
，
的值，并补全频率分布直方图（如图(2)）．
（2）该营销部门为了进一步了解这
名网友的购物体验，从“非网购达人”、“网购达人”中用分层抽样的方法确定
人，若需从这人中随机选取
人进行问卷调查．设
为选取的人中“网购达人”的人数，求的分布列和数学期望．
（1）
（2）
解析试题分析：
（1）已知“非网购达人”与“网购达人”人数比恰好为和总人数60，就可以建立关于各组频数的两个式子，解方程即可得到x,y的值.有了各组的频数,再利用频数除以总数就可以得到频率,频率除以组距就可以得到频率分布直方图中未知分组的纵坐标.
（2）利用抽样过程中每个个体入样可能性相等的条件可以求出“非网购达人”、“网购
达人”各抽取6人和4人.十人中选取三人,则的值有1,2,3.三种情况可以利用无序的组合数和古典概型的概率计算公式求得各种情况的概率,进而建立分布列,得到期望.
试题解析：
（1）根据题意，有
解得
2分
，
．
补全频率分布直方图如图所示． 4分
（2）用分层抽样的方法，从中选取
人，则
其中“网购达人”有
人，“非网购达人”有
人． 6分
故
的可能取值为0，1，2，3； 
， 
，
，
． 10分
所以
的分布列为：
． 12分
考点：分层抽样、概率、随机变量分布列 数学期望
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
气象部门提供了某地区今年六月份(30天)的日最高气温的统计表如下：
| 日最高气温t(单位：℃) | t≤22 | 22＜t≤28 | 28＜t≤32 | t＞32 |
| 天数 | 6 | 12 | Y | Z |
某水果商根据多年的销售经验，六月份的日最高气温t(单位：℃)对西瓜的销售影响如下表：
| 日最高气温t(单位：℃) | t≤22 | 22＜t≤28 | 28＜t≤32 | t＞32 |
| 日销售额X(单位：千元) | 2 | 5 | 6 | 8 |
(2)若视频率为概率，求六月份西瓜日销售额的期望和方差；
(3)在日最高气温不高于32℃时，求日销售额不低于5千元的概率．
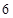瓶饮料中有
瓶已过了保质期.
瓶，求抽到没过保质期的饮料的概率；
，求n的最大值；
的人群随机抽取
人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：
的值；
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动，其中选取2人作为领队，求选取的2名领队中恰有1人年龄在
的概率.
所表示的平面区域内的概率.