题目内容
数列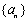 的首项为
的首项为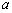 (
( ),前
),前 项和为
项和为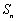 ,且
,且 (
(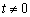 ).
).
设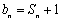 ,
,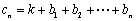 (
(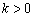 ).
).
(1)求数列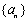 的通项公式;
的通项公式;
(2)当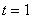 时,若对任意
时,若对任意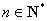 ,
,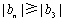 恒成立,求
恒成立,求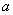 的取值范围;
的取值范围;
(3)当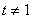 时,试求三个正数
时,试求三个正数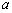 ,
,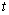 ,
,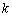 的一组值,使得
的一组值,使得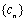 为等比数列,且
为等比数列,且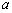 ,
,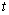 ,
,
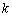 成等差数列.
成等差数列.
(1)因为 ①
①
当 时,
时, ②,
②,
①—②得, (
( ),
),
又由 ,得
,得 ,
,
所以, 是首项为
是首项为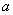 ,公比为
,公比为 的等比数列,所以
的等比数列,所以 (
(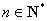 ).
).
(2)当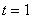 时,
时, ,
, ,
, ,
,
由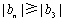 ,得
,得 ,
, (*)
(*)
当 时,
时, 时,(*)不成立;
时,(*)不成立;
当 时,(*)等价于
时,(*)等价于 (**)
(**)
 时,(**)成立.
时,(**)成立.
 时,有
时,有 ,即
,即 恒成立,所以
恒成立,所以 .
.
 时,有
时,有 ,
, .
. 时,有
时,有 ,
, .
.
综上,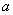 的取值范围是
的取值范围是 .
.
(3)当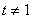 时,
时, ,
, ,
,

 ,
,
所以,当 时,数列
时,数列 是等比数列,所以
是等比数列,所以
又因为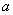 ,
, ,
, 成等差数列,所以
成等差数列,所以 ,即
,即 ,
,
解得 . 从而,
. 从而, ,
, .
.
所以,当 ,
, ,
, 时,数列
时,数列 为等比数列.
为等比数列.

练习册系列答案
相关题目
 ,
, ,
, ,则
,则 .
. 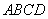 中,
中, ∥
∥ ,
, ,平面
,平面 平面
平面 ,
, 为等边三角形,
为等边三角形, 分别是
分别是 的中点,
的中点, .
.
 ;
; ∥平面
∥平面 ;
; ,求几何体
,求几何体 的体积.
的体积.
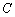 的中心在原点,焦点在
的中心在原点,焦点在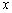 轴上,双曲线
轴上,双曲线 的准线交于
的准线交于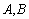 两点,
两点, ,则双曲线C的实轴长为 .
,则双曲线C的实轴长为 .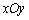 ,圆
,圆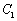 :
: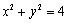 ,圆
,圆 :
: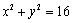 ,点
,点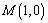 ,动点P、Q
,动点P、Q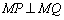 ,则线段
,则线段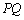 的取值范围是 .
的取值范围是 . ,设
,设 ,其中a,b 均为正实数,证明:h
,其中a,b 均为正实数,证明:h .
. ,N=
,N= ,设曲线y=sinx在矩阵MN对应的变换作用下得到曲线F,求F的方程.
,设曲线y=sinx在矩阵MN对应的变换作用下得到曲线F,求F的方程. =(1,),
=(1,), =(3,m).若向量
=(3,m).若向量