题目内容
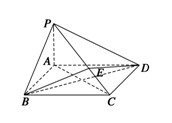
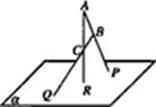
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC= ,AD=1.
,AD=1.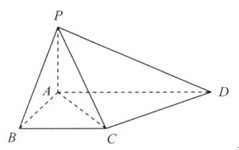
(I)求证:CD⊥平面PAC;
(II)求二面角A-PD-C的余弦值.
(I)见解析;(II)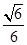 .
.
解析试题分析:(I)先根据已知条件证明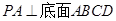 ,那么就有
,那么就有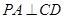 ,在根据题中已知边的长度,由勾股定理证明
,在根据题中已知边的长度,由勾股定理证明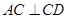 ,根据直线与平面垂直的判定定理即可证明
,根据直线与平面垂直的判定定理即可证明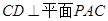 ;(II)设
;(II)设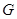 为
为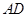 中点,连结
中点,连结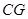 ,过
,过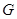 作
作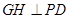 于
于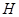 ,证明
,证明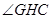 是二面角
是二面角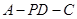 的平面角.再由
的平面角.再由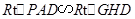 ,解得
,解得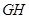 和
和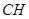 的值,求
的值,求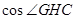 的余弦值即可.
的余弦值即可.
试题解析:(I)∵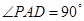 ,∴
,∴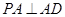 .
.
又∵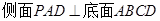 ,
,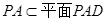 ,且
,且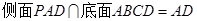 ,
,
∴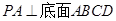 .
.
又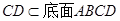 ,∴
,∴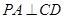 . 3分
. 3分
在底面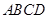 中,∵
中,∵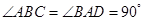 ,
,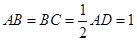 ,
,
∴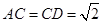 ,有
,有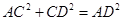 ,∴
,∴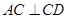 .
.
又∵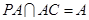 , ∴
, ∴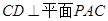 . 6分
. 6分
(II)设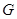 为
为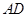 中点,连结
中点,连结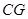 ,则
,则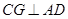 .
.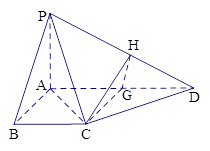
又∵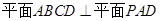 ,
,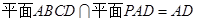 ,
,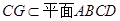 ,∴
,∴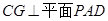 .
.
∵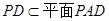 ,∴
,∴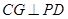 .
.
过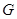 作
作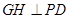 于
于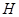 ,
,
∵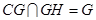 ,∴
,∴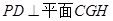 ,
,
∴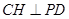 ,∴
,∴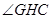 是二面角
是二面角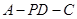 的平面角. 9分
的平面角. 9分
由已知得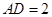 ,
,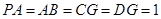 , ∴
, ∴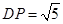 .
.
由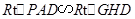 得,
得,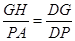 ,∴
,∴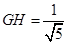 ,
,
∴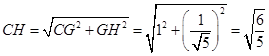 ,
,
∴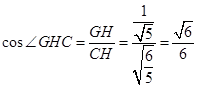 .
.
即二面角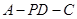 的余弦值为
的余弦值为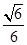 . 12分
. 12分
考点:1、直线与平面垂直的判定定理;2、勾股定理的应用;3、构造二面角;4、平面与平面垂直的性质定理;5、解三角形.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
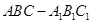 的侧面
的侧面 是菱形,
是菱形,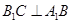
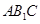
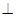 平面
平面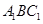 ;
;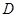 是
是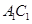 上的点,且
上的点,且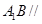 平面
平面 ,求
,求 的值.
的值.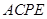 中,
中,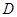 为
为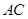 中点,
中点,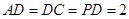 ,
,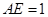 ,且
,且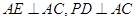 ,现沿
,现沿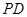 折起使
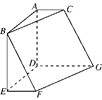
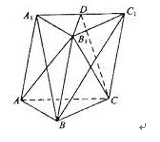
折起使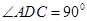 ,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.
,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.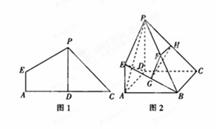
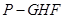 的体积;
的体积;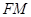 与直线
与直线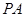 所成角为
所成角为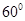 ?若存在,求出线段的长;若不存在,请说明理由.
?若存在,求出线段的长;若不存在,请说明理由.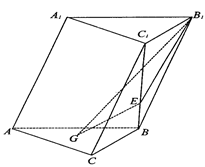

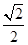 时,求四棱锥P-ABCD的外接球表面积.
时,求四棱锥P-ABCD的外接球表面积.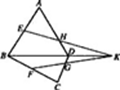
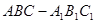 的侧面
的侧面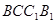 是菱形,
是菱形,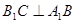 ,D是
,D是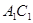 的中点,证明:
的中点,证明: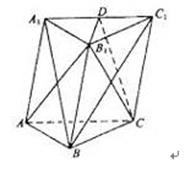
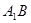 ∥面
∥面
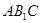
 平面
平面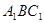 .
.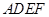 与梯形
与梯形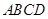 所在平面互相垂直,
所在平面互相垂直,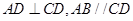 ,
,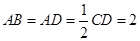 ,点
,点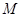 在线段
在线段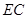 上且不与
上且不与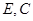 重合。
重合。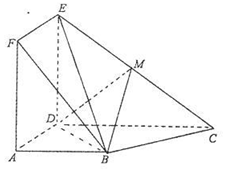
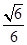 时,求三棱锥
时,求三棱锥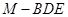 的体积.
的体积.