题目内容
如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为35米,在地面上有一点A,测得A,C间的距离为91米,从A观测电视发射塔CD的视角∠CAD.为45°,则这座电视发射塔的高度CD为 米.
【答案】分析:根据勾股定理求得AB,进而求得tan∠CAB,再通过tan∠DAB=tan(∠DAC+∠CAB)利用正切两角和公式,求得tan∠DAB,再通过tan∠DAB和AB,求得BD,进而求得DC.
解答:解:根据勾股定理可知AB=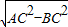 =
=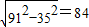 ,
,
∴tan∠CAB=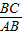 =
=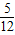 ,
,
∴tan∠DAB=tan(∠DAC+∠CAB)=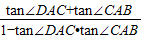 =
=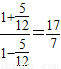 ,
,
∴BD=ABtan∠DAB=204,
∴CD=BD-BC=169,
故答案为:169.
点评:本题主要考查了三角形的实际应用.属基础题.
解答:解:根据勾股定理可知AB=
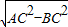 =
=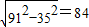 ,
,∴tan∠CAB=
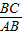 =
=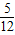 ,
,∴tan∠DAB=tan(∠DAC+∠CAB)=
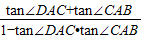 =
=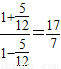 ,
,∴BD=ABtan∠DAB=204,
∴CD=BD-BC=169,
故答案为:169.
点评:本题主要考查了三角形的实际应用.属基础题.

练习册系列答案
相关题目
 如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为35米,在地面上有一点A,测得A,C间的距离为91米,从A观测电视发射塔CD的视角∠CAD.为45°,则这座电视发射塔的高度CD为
如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为35米,在地面上有一点A,测得A,C间的距离为91米,从A观测电视发射塔CD的视角∠CAD.为45°,则这座电视发射塔的高度CD为 如图,某城市的电视发射塔CD建在市郊的小山上,小山的高为60m,在地面上有一点A,测得A、C间的距离为100米,从A观测电视发射塔的视角45°(∠CAD=45°),则这座电视发射塔的高度是
如图,某城市的电视发射塔CD建在市郊的小山上,小山的高为60m,在地面上有一点A,测得A、C间的距离为100米,从A观测电视发射塔的视角45°(∠CAD=45°),则这座电视发射塔的高度是
 ),则这座电视发射塔的高度是_______m;
),则这座电视发射塔的高度是_______m;

