Question

16．对于四面体A-BCD，有以下命题：
①若AB=AC=AD，则AB，AC，AD与底面所成的角相等；
②若AB⊥CD，AC⊥BD，则点A在底面BCD内的射影是△BCD的内心；
③四面体A-BCD的四个面中最多有四个直角三角形；
④若点A到底面三角形BCD三边的距离相等，则侧面与底面所成的二面角相等；
⑤若四面体A-BCD是棱长为1的正四面体，则它的内切球的表面积为$\frac{π}{6}$．
其中，正确的命题是①③⑤（写出所有正确命题的编号）．

Answer 1

分析 对于①，根据线面角的定义即可判断；
对于②，根据三垂线定理的逆定理可知，O是△BCD的垂心，
对于③在正方体中，找出满足题意的四面体，即可得到直角三角形的个数，
对于④点A在平面BCD内射影是△BCD的内心，即可判断，
对于⑤作出正四面体的图形，球的球心位置，说明OE是内切球的半径，利用直角三角形，逐步求出内切球的表面积．

解答 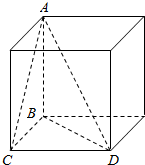解：对于①，因为AB=AC=AD，设点A在平面BCD内的射影是O，因为sin∠ABO=$\frac{AO}{AB}$，sin∠ACO=$\frac{AO}{AC}$，sin∠ADO=$\frac{AO}{AD}$，所以sin∠ABO=sin∠ACO=sin∠ADO，即则AB，AC，AD与底面所成的角相等；故①正确；
对于②设点A在平面BCD内的射影是O，则OB是AB在平面BCD内的射影，因为AB⊥CD，根据三垂线定理的逆定理可知：CD⊥OB 同理可证BD⊥OC，所以O是△BCD的垂心，故②不正确；
对于③：如图：直接三角形的直角顶点已经标出，直角三角形的个数是4．故③正确
对于④，四面体A-BCD，点A到三边距离相等，则点A在平面BCD内射影是△BCD的内心，所以侧面与底面所成的二面角不相等．故④不正确．
对于⑤如图O为正四面体ABCD的内切球的球心，正四面体的棱长为：1；
所以OE为内切球的半径，BF=AF=$\frac{\sqrt{3}}{2}$，BE=$\frac{\sqrt{3}}{3}$，
所以AE=$\sqrt{{1}^{2}-（\frac{\sqrt{3}}{3}）^{2}}$=$\frac{\sqrt{6}}{3}$，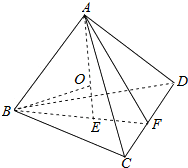
因为BO²-OE²=BE²，
所以（$\frac{\sqrt{6}}{3}$-OE）²-OE²=（$\frac{\sqrt{3}}{3}$）²，
所以OE=$\frac{\sqrt{6}}{12}$，
所以球的表面积为：4π•OE²=$\frac{π}{6}$，故⑥正确．
故答案为：①③⑤

点评 本题考查命题的真假判断与应用，综合考查了线面、面面垂直的判断与性质，考查了学生的空间想象能力，是中档题．